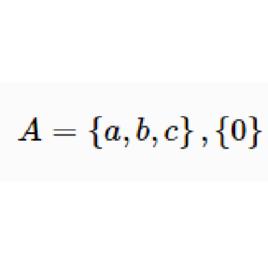定義
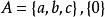 非空集合
非空集合如果一個集合不是空集,那么這個集合叫做非空集合,例如 都是非空集合。
相關概念
集合
集合是數學的基本概念之一。它是現代數學的基礎。把具有某種屬性的一些對象,看做一個整體,便形成一個 集合,集合簡稱 集。
例如:(1)育英國小一年級的全體學生可以形成一個集合;(2)全體自然數也形成一個集合;(3)中國古代的四大發明形成一個集合。
集合一般用大寫字母A,B,C……表示。
集合的元素
組成集合的各個對象,叫做 集合的元素。
例如:(1)育英國小一年級學生的集合是由它的每一個學生作為它的元素的;(2)1,2,3,……是自然數集的元素;(3)指南針,火藥,印刷術,造紙都是中國古代的四大發明集合的元素。
一般地,用小寫字母a,b,c,……表示集合的元素。
元素和集合的關係
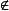 非空集合
非空集合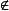 非空集合
非空集合如果a是集合A的元素,就說元素a屬於集合A,記作a∈A。符號“∈”表示屬於,讀作“a屬於A”,或讀作“A含有a”;如果a不是集合A的元素,就說a不屬於A,記作a A.符號“ ”表示不屬於,讀作"a不屬於A",或讀作“A不含有a”。
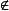 非空集合
非空集合 非空集合
非空集合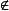 非空集合
非空集合例如,自然數集合用N表示,那么1∈N.3∈N,0N,N……
集合的表示法
集合通常有下列三種表示方法:
(1) 列舉法 把集合中的元素一一列舉出來.寫在{ }裡面。
例1 6的正約數的集合A.可表示為:A={1,2,3,6}
(2) 描述法 把集合中的元素的共同特徵描述出來,寫在{ }裡面。
例2 全體奇數的集合C,可表示為:C={x|x=2n+1,n是整數}。
(3) 文氏圖 法 把集合中的所有元素用一條封閉曲線圈起來表示集合的方法,叫做 文氏圖法。
例3 用a,b,c,d四個元素組成的集合,可以用文氏圖表示。如下圖左。
 圖 1
圖 1例4 組成中國國旗圖案的顏色的集合,可以用文氏圖表示,如上圖右。
有限集
由有限個元素組成的集合,叫做 有限集。
例如,小於1000的自然數的集合A,即A={1,2,3,…,999}={x|x<1000,x是自然數},它是一個有限集。
無限集
由無限個元素組成的集合,叫做 無限集。
例如,自然數的集合,整數集,奇數集,偶數集等都是無限集。
空集
 非空集合
非空集合一個元素也沒有的集合,叫做空集。空集常用表示。
 非空集合
非空集合例如,{小於零的自然數}=。
單元素集
由一個元素組成的集合,叫做單元素集。
例如,由a組成的集合:{a}是一個單元素集合,又如,由0組成的集合:{0}是一個單元素集合。
子集
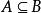 非空集合
非空集合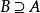 非空集合
非空集合如果集合A的任何一個元素都是集合B的元素,那么集合A叫做集合B的子集。記作或,讀作“A包含於B”。或“B包含A”。
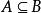 非空集合
非空集合例如,A={1,2,5},B={1,2,3,5,7},由於集合A的每一個元素都是集合B的元素。所以A是B的子集,即。
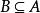 非空集合
非空集合又如,A={三角形},B={等腰三角形}.那么。
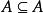 非空集合
非空集合注意:對於一個集合A.因為它的每一個元素都屬於它本身,所以有,也就是說,任何一個集合都是它本身的子集。另外空集是任何一個集合的子集。
真子集
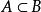 非空集合
非空集合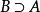 非空集合
非空集合如果集合A是集合B的子集,並且集合B中至少有一個元素不屬於集合A,那么集合A叫做集合B的真子集,記為或。讀作A真包含於B或B真包含A。
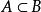 非空集合
非空集合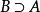 非空集合
非空集合例如:A={1,2,5},B={1,2,3,5,7},集合A是集合B的子集。而集合B中至少有一個元素(元素3)不屬於集合A,所以集合A是集合口的真子集,即或。
相等集
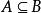 非空集合
非空集合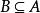 非空集合
非空集合對於兩個集合A與B,如果,同理,我們就說這兩個集合相等,記作A=B,讀作“A等於B”。
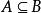 非空集合
非空集合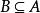 非空集合
非空集合例如;A={0,1,2},B={2,0,1},由於集合A中的每一個元素都是集合B的元素,說明集合A是集合B的子集,即。同理,,所以A=B。
交集
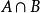 非空集合
非空集合由集合A與集合B的所有共同元素組成的集合,叫做集合A與集合B的交集。記作,讀作A交B。用文氏圖表示如圖2(陰影部分):
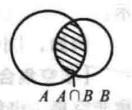 圖 2
圖 2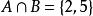 非空集合
非空集合例如,A={1,2,3,5,7},B={2,5,6,10},那么
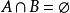 非空集合
非空集合又如,A={1,3},B={4,5,6}那么,文氏圖表示如圖3:。
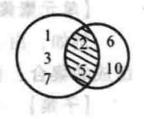 圖3
圖3並集
 非空集合
非空集合由集合A和集合B的所有元素組成的集合,叫做集合A和集合B的並集,記作,讀作A並B。用文氏圖表示如下:(陰影部分)
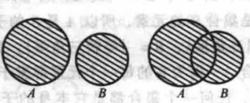 圖4
圖4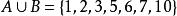 非空集合
非空集合例如,A={1,2,3,5,7},B={2,5,6,10},,文氏圖表示如下:
 圖5
圖5