概念
標準緯線可根據製圖區域而定，也可根據投影條件圖解求得。編制中國全圖時，通常採用雙標準緯線圓錐投影，兩條標準緯線一般取：25°00′、47°00′。
一種基於標準緯線變更的瓦片索引方法
瓦片金字塔模型技術是電子地圖發布的主要技術手段之一，它採用預生成思想將地圖進行橫向分塊和縱向分級，然後根據用戶請求，動態檢索相應的地圖瓦片並自動完成調度與拼接。國內外學者對瓦片金字塔模型的空間劃分和索引方法進行了大量研究，但很少涉及地圖瓦片的投影變形問題。在電子地圖的多尺度表達中，瓦片索引本質上是地圖投影變換和空間索引的融合運用，索引模型的建立需要根據電子地圖所要表達的區域和範圍特點，進行適當的投影變換或變形糾正，以達到客觀表達現實世界的目的。因此，地圖投影變換機制下的瓦片索引方法研究是適應新型地圖產品而派生的新的研究領域，也是地圖投影學研究的一個延伸。
地圖瓦片索引與投影變形
地圖瓦片索引的建立過程主要包括以下兩個步驟：①選擇地圖投影；②結合投影變換和空間索引建立瓦片索引模型。WebMercator投影和Plattecarree投影在基於瓦片索引技術的網路電子地圖發布中套用非常廣泛。由於任何投影變換都會產生不同程度的變形，包括經線的長度變形比m、緯線的長度變形比n、面積P和角度ω的變形。
基於標準緯線變更的瓦片索引算法
建立在WebMercator和Plattecarree兩種投影基礎上的瓦片索引方法套用最為廣泛。但當其套用於世界範圍的電子地圖表達時，高緯度地區存在嚴重的投影變形。為實現算法簡單且變形程度相對較小的瓦片索引算法，本研究在等距圓柱投影的基礎上，實現了一種間斷性變更標準緯線的非固定倍率瓦片索引方法。
（1）算法設計要求
在算法的具體設計過程中，既要減小投影變形，又要避免拼合瓦片時可能引起的“裂縫”。消除相鄰瓦片之間的“裂縫”，需要在同一級別的瓦片劃分過程中保證每一行瓦片跨越的緯度或每一列瓦片跨越的經度相等。
（2）等角條件約束
假定地球為球體，地球的半徑為R，則有：
每一緯度跨越的距離=πR/180
每一經度跨越的距離=πR/180cosα
瓦片的長寬是固定的，當它代表的經緯度滿足實際的長寬比例關係時，就能保證地理要素不發生角度變形。定義具有等角條件的緯度線為標準緯線，並在其適用的緯度帶內定義瓦片代表的經緯度數值。如以武漢市（29°58′N～31°22′N）為例，可定義標準緯線為30°40′N。當表達世界地圖時，為計算的方便，採用0°、±10°、±20°、±30°、±40°、±50°、±60°作為標準緯線，分別用於計算標準緯線±5°範圍的緯度步長。瓦片金字塔的經度步長數組採用非等比數列{90，40，20，10，5，2，1，0.5，0.2，0.1，…，n}，不同緯度帶地圖瓦片跨越的緯度步長等於對應的經度步長乘以該緯度帶內標準緯線緯度的餘弦值。
（3）標準緯線的分帶與特徵值計算
在緯度帶相鄰處，瓦片所代表的緯度數值需取分界線的緯度，以避免拼接時“裂縫”現象的發生。因此，在瓦片劃分過程中，標準緯線所控制計算的區域並非嚴格按照±5°的緯度帶處理，而是取相鄰緯度帶邊界的具體緯度值。在緯度高於55°的緯度範圍內，採用當前經度乘以cos60°作為緯線方向的步長。
以全球範圍的2、3級的瓦片劃分為例，第2級瓦片在北半球將分為3個緯度帶：0°～40°，40°～40°×（1+cos40°），40°×（1+cos40°）～40°×（1+cos40°+cos60°）。按照cos40°=0.766計算，3個緯度帶分別為：0°～40°，40°～70.64°，70.64°～90.64°。北半球最高緯度為90°，因此，劃分後的瓦片需要進行垂直方向（90°－70.64°）/（40°×cos60°）的壓縮，壓縮率大約為0.97。而第3級北半球最高緯度的拼接處緯度值為86.97°，瓦片垂直方向壓縮率為（90°－86.97°）/（20°×cos60°）=0.303。
研究結論
間斷性變更標準緯線的索引方法所引發的地圖變形與WebMercator投影和Plattecarree投影相比，具有以下特點。
1）在經線方向，該算法引起的變形呈不連續跳躍式增長，總體變形程度明顯優於WebMercator投影；
2）在緯線方向，3種算法引起的變形相同；
3）在面積變形方面，該算法引起的變形程度處於WebMercator投影與Plattecarree投影之間，面積總體變形相對較小；
4）在角度變形方面，該算法引起的變形呈回歸曲線型跳躍式增長，在標準緯線處為零，在緯度帶分界處達到周期最高值，整體角度變形明顯優於Plattecarree投影。
一種正軸等角割圓錐投影標準緯線的求算方法
在正軸等角割圓錐投影的建立過程中，人們通常需要預先指定製圖區域內一條或兩條投影后無長度變形的緯線作為地圖投影的標準緯線。比如，在很多知名GIS軟體和RS軟體中要創建正軸等角割圓錐投影則須預先指定其標準緯線；有時候也需要根據現有的地圖投影或地圖來確定其標準緯線的位置。但是，對這一條或兩條標準緯線位置的確定，尚無精確、通用且快捷的方法。由於製圖區域南北跨度、不同製圖要求下地球橢球體參數以及變形條件的差異，不同情況下標準緯線的經驗公式之間也存在著較大差別。這些經驗公式不可能在任何變形條件下都通用。求算精度相對較高的圖解法等近似方法由於計算量大，提出之後沒有被立即轉換為計算機算法，因此未被廣泛採用。為此，本文基於分級遍歷的思想提出了一種在任何變形條件下都通用，且滿足任意精度要求的求算正軸等角割圓錐投影標準緯線的算法。
常規確定方法
在Gauss提出等角割圓錐投影的嚴格公式之前，法國人使用它的近似公式作為軍事地圖的數學基礎，他們通常指定製圖區域距南北邊緯線向製圖區域中心各1/6處作為標準緯線。與六分法不同，用四分法確定標準緯線的方法在國內的教科書中十分常見：取製圖區域距南北邊緯線向製圖區域中心各1/4處為投影的標準緯線。
對緯度跨度固定的地圖，如1∶100萬地形圖，也可採用絕對值作為標準緯線與邊緯線的距離。如，國際上規定1∶100萬地圖的標準緯線為：
φ=φ+40′
φ=φ-40′
式中：φ表示第一條標準緯線；φ表示第二條標準緯線；φ表示北邊緯線；φ表示南邊緯線。
國內採用邊緯線與中緯線長度變形絕對值相等的正軸等角割圓錐投影作為1∶100萬地形圖的數學基礎：
φ≈φ+35′
φ≈φ-35′
如果需要較為精確地確定等角割圓錐投影標準緯線的位置，可以採用圖解法。具體做法：由已知條件計算投影常數α、K和投影的緯圈半徑ρ，並計算出各條緯線的長度比，再以緯度φ和長度比n為坐標軸畫出長度比曲線，從而根據長度比曲線解出標準緯線。
也可以常用的製圖區域建立這些區域的投影集，在需要時查投影集得出標準緯線，這實際上是對圖解法等近似方法的進一步套用。建立投影集的方法顯然不能滿足所有製圖區域及一些特殊變形條件下對標準緯線的求算要求。
分級遍曆法確定等角割圓錐投影的標準緯線
分級遍曆法的基本思想是：根據變形條件求算出α和K，並將求算精度劃分為若干等級，再以α和K為依據，從特定的緯線開始，以劃分好的不同精度由粗到精依此遍歷求算各條緯線上長度比n的值，n值最接近1處的緯線即定為標準緯線。在分級精度中，最高精度決定了標準緯線的求算精度，當最高精度無限接近於0時，可認為得到了標準緯線的嚴格解。具體算法為：
1)根據一定的變形條件，求算出投影常數α和K值。
2)對給定的求算精度λ，選定λ>λ>…>λ>0，使λ=λ。
3)參照經驗公式，初步確定標準緯線φ和φ。
4)如果長度比n(φ)>1，則以λ為步長向北遍歷，求取緯線φ，使n(φ)≤1，比較n(φ)和n(φ+λ)，取n值更接近於1的緯線為φ′。如果n(φ)<1，則以λ為步長向南遍歷，求取緯線φ，使n(φ)≥1，比較n(φ)和n(φ-λ)，取n值更接近於1的緯線為φ′。在遍歷過程中，如果緯度φ處n值恰好等於1，則停止遍歷，直接指定φ為第一條標準緯線的緯度。
5)以λ為步長，重複上一步，由n值更接近於1的緯線代替原φ′。
6)依此類推，直到以λ為步長的遍歷完成，並得出新的φ′。
7)最後得出的φ′即為第一條標準緯線φ。
研究結論
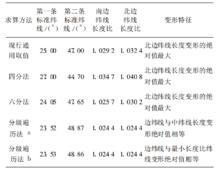表1 不同方法的結果比較( 以中國陸地部分為例)分級遍曆法算法簡單，計算機實現容易，可以滿足任意精度要求、任何變形條件下標準緯線的求算要求。例如，求算中國陸地部分(18°09′N～53°33′N)正軸等角割圓錐投影的標準緯線，採用克拉索夫斯基橢球體，要求投影區域邊緣緯線與最小長度比緯線變形絕對值相等，求算精度為1×10-10°，測試得出只需要遍歷緯線66條，運算耗時平均約0.02 s。求算精度遠遠大於任何現有理論及實踐工作的需要，運算耗時幾乎可以忽略不計。在極高求算精度下，求算的準確性主要取決於地球橢球體參數以及圓周率π的取值。
表1是對分級遍曆法和一些常規方法求算中國陸地部分標準緯線的結果的比較。由表1可以看出，由於採用了精確的計算方法而不是純粹採用經驗公式來確定標準緯線，用分級遍曆法所求得的標準緯線與用傳統方法得出的標準緯線存在著一定差別；同時，它也更能夠滿足正軸等角割圓錐投影的特殊變形尤其是均勻變形的需要。如果需要對標準緯線進行精確求算，或者對尚沒有對其正軸等角割圓錐投影展開專門研究的區域(如中國西北乾旱半乾旱地區等)進行正軸等角割圓錐投影，可以使用本方法。同時，由於割圓錐投影各緯線上的長度比都呈現出在標準緯線之間小於1，在標準緯線之外大於1，且距離標準緯線越遠，長度變形就越大的特點。因此，本算法稍加改變，也同樣適用於其它割圓錐投影標準緯線的求算。
