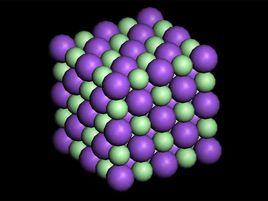
介紹
晶體構架機構即晶體的微觀結構,是指晶體中實際質點(原子、離子或分子)的具體排列情況。自然界存在的固態物質可分為晶體和非晶體兩大類,固態的金屬與合金大都是晶體。晶體與非晶體的最本質差別在於組成晶體的原子、離子、分子等質點是規則排列的(長程式),而非晶體中這些質點除與其最相近外,基本上無規則地堆積在一起(短程式)。金屬及合金在大多數情況下都以結晶狀態使用。晶體構架機構是決定固態金屬的物理、化學和力學性能的基本因素之一。
周期性
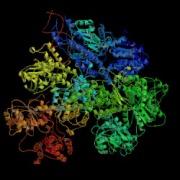 構架結構
構架結構晶體是各向異性的均勻物體。生長良好的晶體,外觀上往往呈現某種對稱性。從微觀來看,組成晶體的原子在空間呈周期重複排列。即以晶體中的原子或其集合為基點,在空間中三個不共面的方向上,各按一定的點陣周期,不斷重複出現。如從重複出現的每個基元中各取某一相當點,則這些點合在一起形成一個空間點陣的一部分。確切地說,點陣是一組按連線其中任何兩點的矢量進行平移後而能復原的點的重複排列。
空間點陣是認識晶體構架機構基本特徵的關鍵之一,用它可以方便而又清楚地說明晶體的微觀結構在巨觀中所表現出的面角守恆、有理指數等定律以及X射線衍射的幾何關係。各點分布在同一直線上的點陣稱為直線點陣,分布在同一平面中者稱為平麵點陣,而分布在三維空間中者稱為空間點陣。空間點陣可以分解為各組平行的直線點陣或平麵點陣,並可劃分成並置的平行六面體單位。規定這個單位的矢量為 a、 b和 c。空間點陣劃分成一個個並置的平行六面體單位後,若點陣中各點都位於各平行六面體的頂點處,則此單位只攤到一個點,稱為素單位。平行六面體單位也可在面上或體內帶心,攤到一個以上的點,成為復單位。按照空間點陣的平行六面體單位,可劃分成晶體構架機構的單位,這樣的單位稱為晶胞。
晶體的一些巨觀規律性反映了它微觀結構中具有長程式的空間點陣形式。晶體之所以不同於一般具有短程式的非晶態固體和液體而成為各向異性體,與此有關。晶體外形為晶面構成的多面體,而晶面必與空間點陣中一組平麵點陣平行,晶棱則與某一直線點陣組平行。在同一種晶體上兩個給定晶面之間的交角是兩組相應的點陣平面之間的交角,從而是常數。
點陣平面和直線點陣方向的表示方法在任何晶體中,可根據空間點陣的基向量 a、 b和 c來取晶軸系。若任一點陣平面與它們交於A、B和C,則這個面在這三個晶軸上的倒易截之比,必可通約成三個互質數之比,即 h: k: l,這是“有理指數定律”, h, k, l稱為點陣平面指數,而( h k l)是該晶面的符號。晶棱或與一組直線點陣平行的方向可用記號【 u v w】來代表,其中 u、 v和 w也是三個互質的整數,稱點陣方向指數。而這個方向與矢量 u a+ v b+ w c平行。例如直線點陣方向【100】必與 a平行,【010】與 b平行,等等;而點陣平面(100)必與 b和 c平行,(010)與 c和 a平行,等等。
有了點陣概念就可以將晶體構架機構用下述所謂公式來簡單表示:
晶體構架機構=點陣+結構基元
晶體對稱性
在晶體的外形以及其他巨觀表現中還反映了晶體構架機構的對稱性。晶體的理想外形或其結構都是對稱圖象。這類圖象都能經過不改變其中任何兩點間距離的操作後復原。這樣的操作稱為對稱操作,平移、旋轉、反映和倒反都是對稱操作。能使一個圖象復原的全部不等同操作,形成一個對稱操作群。在晶體構架機構中空間點陣所代表的是與平移有關的對稱性,此外,還可以含有與旋轉、反映和倒反有關並能在巨觀上反映出來的對稱性,稱為巨觀對稱性,它在晶體構架機構中必須與空間點陣共存,並互相制約。制約的結果有二:①晶體構架機構中只能存在1、2、3、4和6次對稱軸,②空間點陣只能有 14種形式。 n次對稱軸的基本旋轉操作為旋轉360°/ n,因此,晶體能在外形和巨觀中反映出來的軸對稱性也只限於這些軸次。
類型
根據晶體的巨觀對稱性,布喇菲(Bravais)在1849年首先推導出14種空間點陣,它們的晶軸關係即晶軸的單位長度及夾角(即單胞參量 a、 b、 c、 α、 β、 γ)間的關係,分別屬於立方、四方、三方、六方、正交、單斜、三斜共7個晶系(見表)。其中立方晶系的對稱性最高,晶胞的三個邊等長( a= b= c)並正交( α= β= γ=90°)。三斜晶系的對稱性最低 ( a≠ b≠ c, α≠ β≠ γ≠90°)。在四方晶系中,晶胞的兩個邊等長並正交;而在正交晶系中三個邊皆不等長。在六方晶系中,兩個邊等長( a= b≠ c),它們的夾角 γ=120°,而在三方晶系的菱面體晶胞中,三個邊等長,三個夾角相等,但無正交關係(三方晶系中也可取六方點陣的晶胞),在單斜晶系,三個邊不等長,三個夾角中有兩個是90°。在這7個晶系中,除了由素單位構成的簡單點陣(P)外,還可能有體心(I)、底心(C)、面心(F)點陣。在這些有心的點陣中,晶胞分別有2個或4個陣點。
類型
晶體可以由原子、離子或分子結合而成。例如非金屬的碳原子通過共價鍵可以形成金剛石晶體。金屬的鈉原子與非金屬的氯原子可以先分別形成Na和Cl離子,然後通過離子鍵結合成氯化鈉晶體,每個離子周圍是異號離子。離子結合而成的晶體稱為離子晶體。在有些晶體中原子可以先結合成分子,然後通過分子間鍵或范德華(Van der Waals)力結合成晶體。如非金屬的硫原子先通過共價鍵形成王冠狀的S8分子,然後再通過范德華力形成硫黃晶體。又如在石墨中碳原子先通過共價鍵形成層型分子,然後通過范德華力結合成晶體。在層型分子內部,化學鍵是連亘不斷的。礦物主要以金屬氧化物、硫化物以及矽酸鹽晶體的形式存在,它們一般為離子晶體。金屬原子通過金屬鍵結合而成金屬晶體。典型結構有A1、A2和A3型等三種。晶體中每一原子周圍所具有的,與其等距離的最近鄰的原子數目叫配位數。
在這三種結構型式中,每個原子為很多相同的原子所包圍,從而配位數很高。考慮金屬學問題往往採用一個較簡單的模型,即把金屬原子(離子實)看成是剛性球體,它們之間相互吸引,從而結合在一起。如果將上述的金屬典型結構與等徑剛球三種較密的排列方式相對應,如圖4所示,與A1和A3型相應的各為立方和六方最密排列,每個剛球與周圍的12個剛球鄰接,配位數記為12。與A2型相應的是立方體心密排,每個剛球為周圍8個剛球相包圍,此外,尚有6個次近鄰剛球,距離只比8個最近鄰遠15%左右,因此往往要考慮到次近鄰的作用。有時將A2型的配位數記為8+6,即有效配位數要大於 8。在上述密排結構中存在兩種間隙位置,即四面體間隙和八面體間隙。在某些條件下,這些間隙空間可成為金屬或合金中自身的或外來的原子所在位置,例如碳就可以占據鐵點陣中的間隙位置。除了上述三種常見的晶體構架機構之外,金屬元素還有其他幾種結構,如正交結構(如鎵、鈾)、四方結構(如銦、鈀)、菱面體結構(如鉀、銻、鉍)等。