簡介
極限集理論是定性理論的重要基礎之一。
ω極限集
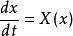 極限集理論
極限集理論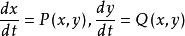 極限集理論
極限集理論考慮系統或平面系統。
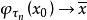 極限集理論
極限集理論 極限集理論
極限集理論從x點出發的軌線φ(x),若存在序列t→+∞,使得,則稱為軌線φ(x)的ω極限點,稱φ(x)的所有ω極限點的集合為φ(x)的ω極限集,記為L(x)。
α極限集
類似地,考察t→-∞的情況,則可得出α極限點與α極限集的定義。φ(x)的α極限集記為L(x)。
結論
由上述定義易見,奇點x是φ(x)=x的惟一的ω和α極限點,閉軌φ(x)上的任一點都是此閉軌的ω和α極限點。亦即,奇點和閉軌分別為它們自身的ω和α極限集。
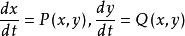 極限集理論
極限集理論對於平面定常系統,極限集理論有甚為清晰完整的結論,可歸結如下:若系統的一條正半軌φ(x)(t≥0)保持在有界區域D內,則L(x)必屬於下列情形之一:
1一個奇點;
2一條閉軌;
3一條奇閉軌。
由此即可推出龐加萊-本迪克松定理。
定性理論
定性理論又稱“微分力一程定性理論”,“幾何理論”,是根據全而分析微分力一程所確定的積分曲線的整體分布狀況來研究解的性質的理論。
迄今定性理論仍以二階為主,主要內容是分析奇點,極限環的個數,位置和軌線的走向。在力學,天體力學等工程技術領域有廣泛的套用。
