簡介
在數學中，特別是在動態系統理論里，一個二維平面或二維流形上的極限環是相空間裡的一個閉合的軌跡，使得至少另一個軌跡會隨自變數變化而逐漸逼近它（在自變數趨於正無窮或負無窮的時候）。
如果當自變數（或者說時間）： t趨於正無窮時，所有的鄰近軌跡都趨近於極限環，那么所在的流形被稱為穩定的，或者稱極限環是穩定的（吸引的）。反之，如果 t趨於負無窮時，所有的鄰近軌跡都趨近於極限環，那么稱流形是不穩定的或者極限環是不穩定的（非吸引的）。在所有其它情況下，流形既不是穩定也不是不穩定的。
穩定的極限環會導致持續振盪的情況：若一開始軌跡是極限環，則關於軌跡的任意的小擾動都會導致系統重新回到極限環的狀態。
基本概念
定義1：
對於平面自治系統(1)：
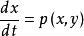穩定極限環
穩定極限環有閉軌線Γ，若存在δ>0使系統(1)在Γ的兩側鄰域S(Γ，δ)內的一切軌線均以Γ為其Ω或A極限集，則稱Γ為系統(1)的一個極限環。
容易看出，這樣定義的極限環實際上就是一條孤立的閉軌線。
定義2：
若系統(1)在其極限環Γ外側(內側)足夠小鄰域內的軌線均以Γ為Ω極限集，則稱Γ為外(內)穩定極限環；
若均以Γ為A極限環，則稱Γ為外(內)不穩定環；
若Γ既外穩定(不穩定)又內穩定(不穩定)，則稱Γ為穩定(不穩定)極限環；
若Γ的一側穩定另一側不穩定，則稱Γ為半穩定極限環。
定義3：
對於系統( 1) 而言，均設
穩定極限環設函式 F( x, y) ∈C (G)，易知曲線族 F( x, y) =C 與軌線相切點的軌跡方程是：
穩定極限環我們稱曲線( 2) 為系統( 1) 的切性曲線。同時，注意到 F( x,y) 沿系統( 1) 的軌線關於 t 的全導數為：
穩定極限環判斷極限環的穩定性的方法
穩定極限環
穩定極限環（1）一種是根據 的符號結合 的表達式
（2）如果沿著系統的極限環Γ有
穩定極限環則Γ是穩定(不穩定)的，其中T是Γ的周期。
舉例
考察系統
穩定極限環
穩定極限環在全平面極限環的存在性及穩定性。
取曲線族：
穩定極限環求得：
穩定極限環所以該系統的切性曲線對應於原點O和單位圓周x +y =1。在單位圓周內，除點O外不含切性曲線上的點，由定理知，單位圓內系統不存在閉軌;同樣單位圓外系統也不存在閉軌。容易驗證，單位圓周是系統的軌線，並且它是唯一穩定的極限環。
