定義
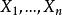 極值分布
極值分布設 為從總體F抽出的獨立同分布樣本,且
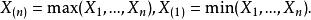 極值分布
極值分布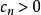 極值分布
極值分布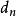 極值分布
極值分布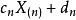 極值分布
極值分布如果存在常數 及 ,使 依分布收斂於G(x),則稱G(x)為一極大值分布;類似地定義極小值分布。它們統稱為 極值分布,而分布F稱為“底分布”。
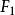 極值分布
極值分布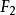 極值分布
極值分布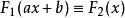 極值分布
極值分布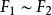 極值分布
極值分布兩個分布函式 和 稱為是同類的,若存在常數a>0及b,使 ,並記為 。
顯然,這種關係具有自反、對稱和傳遞性。
極值分布的三大類型(Fisher—Tippett Theorem):若G(x)為一連續極值分布,則G必與下列三個分布函式之一同類:
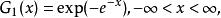 極值分布
極值分布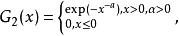 極值分布
極值分布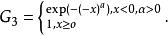 極值分布
極值分布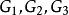 極值分布
極值分布分別稱為第Ⅰ、Ⅱ、Ⅲ型極值分布,也分別稱為Gumbel、Fr6cht、Weibull型極值分布。
一般的Gumbel型極值分布為
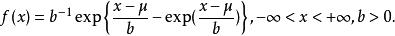 極值分布
極值分布相應的生存函式為
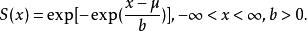 極值分布
極值分布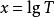 極值分布
極值分布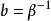 極值分布
極值分布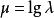 極值分布
極值分布當T服從威布爾分布且有密度函式式一般的Gumbel型極值分布時, 就服從 和眾數為 的一般Gumbel型極值分布。
Gumbel型極值分布
極小值分布
最小極值Ⅰ型分布簡稱極小值分布,其分布密度函式和分布函式分別為
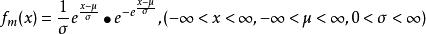 極值分布
極值分布及
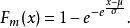 極值分布
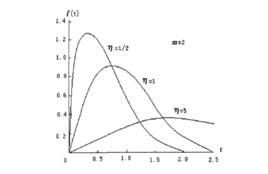
極值分布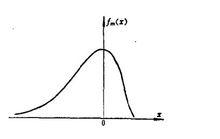 圖1
圖1 極值分布
極值分布 極值分布
極值分布式中 ——位置參數,實際上是分布的眾數; ——尺度參數,與分布的離散性有關。
 極值分布
極值分布 極值分布
極值分布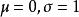 極值分布
極值分布必須注意, 和 不是分布的均值及標準差,但與它們有關,分布密度函式式的圖形見圖1。圖中曲線為 的情況,由圖可知,極小值分布為一偏態分布(右偏)。
1.標準極小值分布,
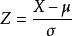 極值分布
極值分布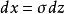 極值分布
極值分布令 ,則 ,代入上述分布密度函式和分布函式式子中得到Z的密度函式及分布函式分別為
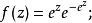 極值分布
極值分布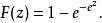 極值分布
極值分布 極值分布
極值分布 極值分布
極值分布上兩式稱為標準極小值分布,並且與分布參數 及 無關。
2.標準極小值分布的期望值及方差,
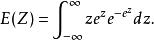 極值分布
極值分布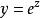 極值分布
極值分布令 ,代入上式得
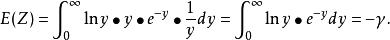 極值分布
極值分布 極值分布
極值分布上式積分為一常數,稱作歐拉(Euler)常數。通常記為“ ”即
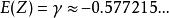 極值分布
極值分布又
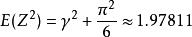 極值分布
極值分布所以
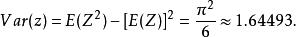 極值分布
極值分布3.極小值分布的期望值及方差,
因為
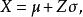 極值分布
極值分布所以
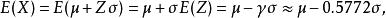 極值分布
極值分布及
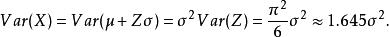 極值分布
極值分布 極值分布
極值分布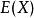 極值分布
極值分布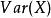 極值分布
極值分布 極值分布
極值分布 極值分布
極值分布如果已知樣本的試驗數據,則可以計算總體的均值及標準差的估計值 及s,再由 和 的等式可以得到極小值分布的位置參數 及尺度參數 的估計值:
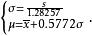 極值分布
極值分布極大值分布
最大極值Ⅰ型漸近分布密度函式和分布函式分別為
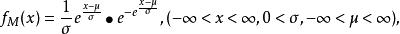 極值分布
極值分布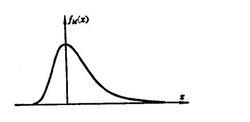 圖2
圖2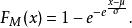 極值分布
極值分布 極值分布
極值分布 極值分布
極值分布式中, ——位置參數; ——尺度參數。
極大值分布密度函式的圖形如圖2所示。
1.標準極大值分布
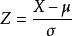 極值分布
極值分布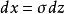 極值分布
極值分布令,則 ,代入最大極值Ⅰ型漸近分布密度函式和分布函式兩式中,得到
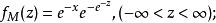 極值分布
極值分布及
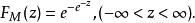 極值分布
極值分布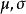 極值分布
極值分布上兩式稱為標準極大值分布密度函式及分布函式,它們與分布參數 無關。
標準極大值分布的期望值及方差分別為
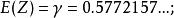 極值分布
極值分布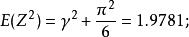 極值分布
極值分布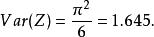 極值分布
極值分布2.極大值分布的期望值和方差
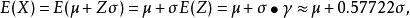 極值分布
極值分布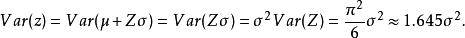 極值分布
極值分布