簡介
由於在數學上成就卓著,他被選為英國皇家學會會員,柏林科學院和巴黎科學院的外籍院士。棣莫佛是牛頓的親密朋友,他的數學才能深受牛頓的推崇。牛頓晚年常常對一些向他請教數學問題的人說:“去找棣莫佛先生吧,他比我更精通這些問題。”作為大數學家,棣莫佛在英國享有盛譽。他的同代人,英國著名詩人波普(A. Pope, 1688~1744)在《人類小品》中吟道:
是誰教那蜘蛛
不用直線或直尺幫忙
畫起平行線來
和棣莫佛一樣穩穩噹噹
詩人筆下的棣莫佛,無疑成了數學家的代名詞了。棣莫佛的死是一個奇蹟,在去世前不久,他聲稱以後每天將比前一天多睡一刻鐘。最後,他睡了二十四小時,從此再也沒有醒來。
公式證明
把複數用三角式(具體參見複數)表示:
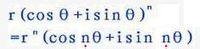 棣莫佛公式
棣莫佛公式棣莫佛定理
c=r(cosa+isina)
證明:
或者表示為:
r(cos+isina) 的n次方根=n次根號下{r×[cos((a+2k)/n)+isin((a+2kπ)/n)]} 其中k=0,1,2...n-1
先引入歐拉公式:e^ix = cosx + isINX
1.將e^t,sint , cost 分別展開為泰勒級數:
e^t = 1 + t + t^2/2! + t^3/3! + …… + t^n/n!+ ……
sint = t - t^3/3!+t^5/5!-t^7/7!+……-……
cost = 1 - t^2/2!+t^4/4!-t^6/6!+……-……
將t = ix 代入以上三式 ,可得歐拉公式
套用歐拉公式,(cosx+isinx)^n = (e^ix)n
=e^inx
=cos(nx)+isin(nx)
證畢
相關
泰勒級數
(cosx+isinx)*(cosy+isiny)=cosx*cosy - sinx*siny +(sinx*cosy +cosx*siny)*i=cos(x+y)+isin(x+y) 令x=y=n 可得 (cosn+isinn)^2 = cos(2n)+isin(2n) 令x=n y=2n,可得 (cosn+isinn)*(cos2n+isin2n)=cos3n+isin3n
