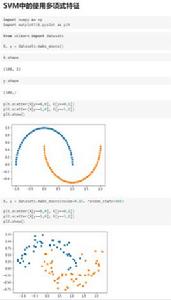
定義
核映射(nuclear map)一類重要的映射,設X是局部凸空間,Y是巴拿赫空間,T是從X到Y的線性映射,如果T有如下表示
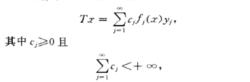 核映射
核映射{f(x)}是X上連續線性泛函序列,{yi}是Y中有界序列,則稱T為核映射。
核方法
所謂核方法,就是確定一個樣本空間中的核函式,並將核空間中的線性運算表示成內積形式,然後用核函式來代替核空間中的內積,從而將核空間中內積所涉及的操作轉換成核函式的操作。核方法通過核函式的操作間接實現從樣本空間到核空間的非線性映射和核空間中的線性子空間降維,從而在本質上實現樣本空間中的非線性運算。
在核方法中,雖然有核映射和核空間的概念,但實際上不必真的去選擇核映射西,也不必真的去計算核空間中的內積,只需選擇核函式,然後用核函式去代替核空間中的內積即可。因此,凡是能用內積表示的線性算法都可通過核方法實現非線性變種。
對於基於核方法的子空間降維來說,要實現這種非線性的子空間算法,有兩個前提:一個是必須能將核空間中的子空間降維所涉及的線性運算表示成內積形式,這將在下面介紹;另一個是核函式的選擇或確定。
目的
由於已知數據的特性,因而能給出適當的核映射。但在實際問題中人們往往不能準確獲知數據的特性,因此如何選擇合適的核映射是一個問題。退一步來說,即使找到了合適的核映射將數據嵌入到核空間中,可要在核空間中實施線性子空間降維仍有問題,這是因為核空間的維數很高甚至無窮,在核空間中直接實施線性子空間降維幾乎不可能。幸運的是,這兩個問題都可通過將核空間中的內積轉化為樣本空間中的核函式來解決。
套用
將核函式與特徵空間中的內積關聯起來這一思想,開始於Aizerman等關於勢函式方法的研究,這種思想直接引起了SVM方法的出現。接著將核函式方法與傳統的數據分析方法結合起來進行研究就相繼出現了,如核主成
分分析、核Fish判別式、核聚類方法等等。
SVM方法是將核方法與構造最優分類器結合起來的一種結構風險最小化方法,通過建立一個合適的核映射,從而將原始樣本空間中的線性不可分問題轉化為高維特徵空間中的線性可分問題。核聚類方法利用Mercer核,把
輸入空問中的樣本映射到高維特徵空間,從而在特徵空間中具有更好的聚類分布性。理論分析和實驗表明該方法是普適的,它通過非線性映射能夠較好地分辨、提取並放大有用的特徵,從而實現更為準確的聚類。
雖然利用核函式可以避開去具體構造一個從原始樣本空間到特徵空間的映射系統,但在最常用的高斯核函式中需要利用樣本空間中任兩個樣品之差的範數,所以,原始樣本空間的合適“距離”定義對於構造一個合適的核映射就起重要作用了。找到一個比較合適的原始樣本空間的“距離”定義對於後續的分類預測也很重要,因為在K最近鄰分類中,尋找最近鄰的代表點就需要計算新數據點與代表數據點之間的“距離”。本章利用核映射將特徵空間中的聚類問題和原始樣本空問中的分類問題聯繫起來,提出一種基於核映射的屬性權重的自適應最佳化方法。通過UCI的兩個數據集的實驗,表明這種方法在套用於屬性選擇、確定屬性權重方面是有效的。