核方法kernel methods (KMs)是一類模式識別的算法。其目的是找出並學習一組數據中的相互的關係。用途較廣的核方法有支持向量機、高斯過程等。
本文對核方法(kernel method)進行簡要的介紹。
核方法的主要思想是基於這樣一個假設:“在低維空間中不能線性分割的點集,通過轉化為高維空間中的點集時,很有可能變為線性可分的” ,例如有兩類數據,一類為x<aUx>b;另一部分為a<x<b。要想在一維空間上線性分開是不可能的。然而我們可以通過F(x)=(x-a)(x-b)把一維空間上的點轉化到二維空間上,這樣就可以劃分兩類數據F(x)>0,F(x)<0;從而實現線性分割。
然而,如果直接把低維度的數據轉化到高維度的空間中,然後再去尋找線性分割平面,會遇到兩個大問題,一是由於是在高維度空間中計算,導致維度禍根(curse of dimension)問題;二是非常的麻煩,每一個點都必須先轉換到高維度空間,然後求取分割平面的參數等等;怎么解決這些問題?答案是通過核戲法(kernel trick)。(pku, shinningmonster, sewm)
 核方法
核方法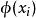 核方法
核方法 核方法
核方法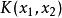 核方法
核方法Kernel Trick:定義一個核函式 <>, 其中x1和x2是低維度空間中點(在這裡可以是標量,也可以是向量),是低維度空間的點轉化為高維度空間中的點的表示,< , > 表示向量的內積。這裡核函式的表達方式一般都不會顯式地寫為內積的形式,即我們不關心高維度空間的形式。
核函式巧妙地解決了上述的問題,在高維度中向量的內積通過低維度的點的核函式就可以計算了。這種技巧被稱為Kernel trick。
這裡還有一個問題:“為什麼我們要關心向量的內積?”,一般地,我們可以把分類(或者回歸)的問題分為兩類:參數學習的形式和基於實例的學習形式。參數學習的形式就是通過一堆訓練數據,把相應模型的參數給學習出來,然後訓練數據就沒有用了,對於新的數據,用學習出來的參數即可以得到相應的結論;而基於實例的學習(又叫基於記憶體的學習)則是在預測的時候也會使用訓練數據,如KNN算法。而基於實例的學習一般就需要判定兩個點之間的相似程度,一般就通過向量的內積來表達。從這裡可以看出,核方法不是萬能的,它一般只針對基於實例的學習。
緊接著,我們還需要解決一個問題,即 核函式的存在性判斷和如何構造? 既然我們不關心高維度空間的表達形式,那么怎么才能判斷一個函式是否是核函式呢?
Mercer 定理:任何半正定的函式都可以作為核函式。所謂半正定的函式f(xi,xj),是指擁有訓練數據集合(x1,x2,...xn),我們定義一個矩陣的元素aij = f(xi,xj),這個矩陣式n*n的,如果這個矩陣是半正定的,那么f(xi,xj)就稱為半正定的函式。這個mercer定理不是核函式必要條件,只是一個充分條件,即還有不滿足mercer定理的函式也可以是核函式。
常見的核函式有高斯核,多項式核等等,在這些常見核的基礎上,通過核函式的性質(如對稱性等)可以進一步構造出新的核函式。SVM是目前核方法套用的經典模型。
