基本介紹
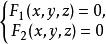 投影柱面
投影柱面設空間曲線C的方程為 過曲線C上每一點作xOy坐標面的垂線,這些垂線形成了一個母線平行於z軸且過曲線C的柱面,這個柱面稱為曲線C關於xOy坐標面的 投影柱面,該投影柱面與xOy面的交線叫做空間曲線C在xOy面上的 投影曲線,簡稱 投影。
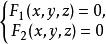 投影柱面
投影柱面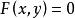 投影柱面
投影柱面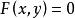 投影柱面
投影柱面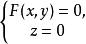 投影柱面
投影柱面在方程組 中消去變數z得到方程 ,該方程中不含z,所以它是一個母線平行於z軸的柱面,又因為曲線C上的點的坐標滿足該方程,所以曲線C上的點都在這個柱面上,方程 就是曲線C關於xOy坐標面的投影柱面方程。它與xOy坐標面的交線 就是曲線C在xOy坐標面上的投影曲線方程。
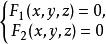 投影柱面
投影柱面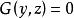 投影柱面
投影柱面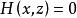 投影柱面
投影柱面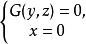 投影柱面
投影柱面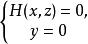 投影柱面
投影柱面同理,若從方程組 中分別消去變數x或y,得到該曲線的投影柱面 或 ,則曲線C在yOz坐標面與xOz坐標面上的投影曲線的方程分別為 與 。
例題分析
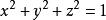 投影柱面
投影柱面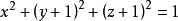 投影柱面
投影柱面例1 已知兩球面的方程為和,求它們的交線C在xOy坐標面上的投影的方程。
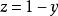 投影柱面
投影柱面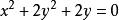 投影柱面
投影柱面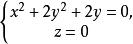 投影柱面
投影柱面解:先求包含交線C而母線平行於z軸的柱面方程,將已知兩球面方程相減得,再代入其中任一個方程,即得所求柱面方程為,這就是交線C關於xOy坐標面的投影柱面方程,於是,兩球面的交線在xOy坐標面上的投影方程為
注意:在重積分和曲面積分的計算中,常常需要確定一個立體或曲面在坐標面上的投影曲線,這時要利用投影柱面和投影曲線。
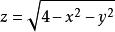 投影柱面
投影柱面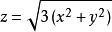 投影柱面
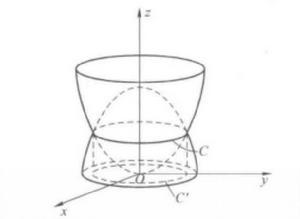
投影柱面例2 設一個立體由上半球面和錐面所圍成(圖1),求它在xOy面上的投影。
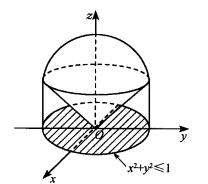 圖1
圖1解:半球面和錐面的交線為
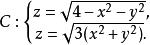 投影柱面
投影柱面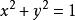 投影柱面
投影柱面由上列方程組消去z,得到。這是一個母線平行於z軸的圓柱面,容易看出,這恰好是交線C關於xOy面的投影柱面,因此交線C在xOy面上的投影曲線為
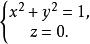 投影柱面
投影柱面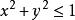 投影柱面
投影柱面這是xOy面上的一個圓,於是所求立體在xOy面上的投影,就是該圓在xOy面上所圍的部分:。
其他詳細分析
設給定一條空間曲線C和通過它的一點的一條直線L,當直線L沿曲線C平行移動所產生的曲面稱為 柱面(圖2),曲線C稱為柱面的 準線,動直線稱為柱面的 母線 。
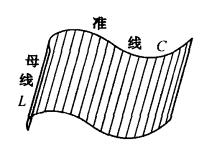 圖2
圖2準線C是圓的柱面稱為 圓柱面。若母線L與準線圓所在平面垂直,這個柱面稱為 正圓柱面(圖3)。
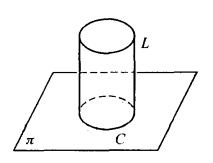 圖3
圖3以下討論母線平行於坐標軸的柱面方程。
在空間直角坐標系中,不含z坐標的方程
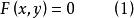 投影柱面
投影柱面表示一個柱面(圖4),其母線平行於z軸,準線是xy平面上的曲線
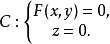 投影柱面
投影柱面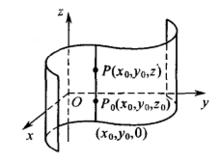 圖4
圖4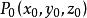 投影柱面
投影柱面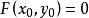 投影柱面
投影柱面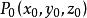 投影柱面
投影柱面事實上,設空間有一點在方程(1)的圖形上,則有。過點作平行於z軸的直線:
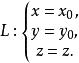 投影柱面
投影柱面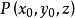 投影柱面
投影柱面L上的所有點的坐標都滿足方程(1),即直線L在方程(1)的圖形上。也就是說,方程(1)的圖形是由平行於z軸的直線組成的,因此它是一個母線平行z軸的柱面,準線是柱面與xy平面的交線
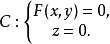 投影柱面
投影柱面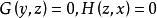 投影柱面
投影柱面同理,方程分別代表母線平行x軸和y軸的柱面。一般來說,在空間直線坐標系中,一個坐標不出現的方程表示母線平行於該坐標軸的柱面。
在空間直角坐標系中,方程
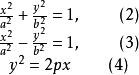 投影柱面
投影柱面都表示母線平行於z軸的柱面。由於這些柱面與xy平面的交線分別是橢圓、雙曲線和拋物線,因此分別稱為 橢圓柱面、 雙曲柱面和 拋 物柱面,它們統稱為 二次柱面(圖5)。
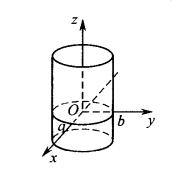 圖5(a)
圖5(a)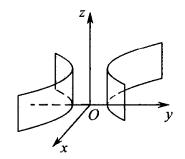 圖5(b)
圖5(b) 圖5(c)
圖5(c)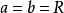 投影柱面
投影柱面在方程(2)中若,可得圓柱面方程 :
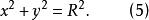 投影柱面
投影柱面