簡介
在數學中，拋物柱面函式是作為微分方程解的一類特殊函式。
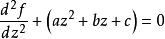拋物柱面函式當在拋物柱面坐標中表示時，在拉普拉斯方程上使用變數分離技術時，發現了該方程。
通過完成稱為H. F.韋伯方程（Weber 1869）的平方和重新縮放z，可以將上述方程式分成兩種不同的形式（A）和（B））：
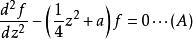拋物柱面函式
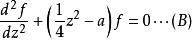拋物柱面函式如果f（a,z）是解，那么f（a,-z）、f（-a,iz）、f（-a,-iz）也都是解。
如果f（a,z）是方程（A）的解，那么f（-ia,ze ）是方程（B）的解，並且類似的，f（-ia,-ze ）、f（ia,-ze ）、f（ia,ze ）也是方程（B）的解。
求解
有（A）形式的獨立偶數和奇數解。 這些是由（阿布拉莫維茨和史蒂文（1965年））給出的 ：
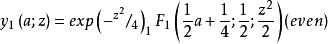拋物柱面函式和
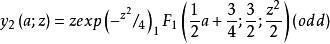拋物柱面函式
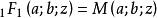拋物柱面函式其中是超幾何函式。
可以由上述解的線性組合形成其他成對的獨立解。 這樣的組合是基於他們在無窮遠的函式：
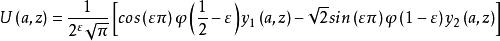拋物柱面函式
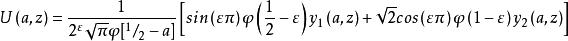拋物柱面函式
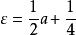拋物柱面函式這裡，。
當| arg（z）|<π/ 2時，函式U（a，z）接近零，而V（a，z）發散。
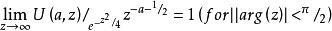拋物柱面函式
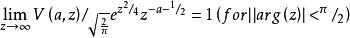拋物柱面函式對於a的整數值，這些（即U和V）可以用Hermite多項式來重新表示；或者，它們也可以用貝塞爾函式來表示。
函式U和V也與拋物柱面函式Dp（x）（可追溯到Whittaker（1902）的符號）有關：
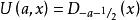拋物柱面函式
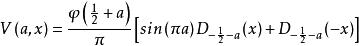拋物柱面函式函式D（a，z）由惠特克和沃森引入，可以用超幾何函式來表示
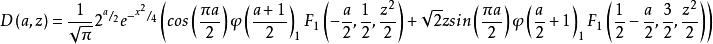拋物柱面函式