簡介
拋物柱面坐標系（英語：Parabolic cylindrical coordinates）是一種三維正交坐標系。往 z-軸方向延伸二維的拋物線坐標系，則可得到拋物柱面坐標系。其坐標曲面是共焦的拋物柱面。拋物柱面坐標可以套用於許多物理問題。例如，物體邊緣的位勢論。
基本定義
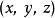拋物柱面坐標系
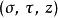拋物柱面坐標系直角坐標 可以用拋物柱面坐標 表示為
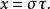拋物柱面坐標系
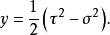拋物柱面坐標系
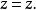拋物柱面坐標系
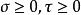拋物柱面坐標系其中， 。
拋物柱面坐標系坐標 為常數的曲線形成共焦的，凹性往 +y-軸的拋物柱面：
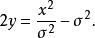拋物柱面坐標系
拋物柱面坐標系而坐標 為常數的曲線形成共焦的，凹性往 -y-軸的拋物柱面：
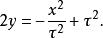拋物柱面坐標系這些拋物柱面的焦線的位置都在 z-軸。
徑向距r的公式為
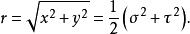拋物柱面坐標系當解析經典力學的反平方連心力問題時，假若採用拋物柱面坐標的哈密頓-亞可比方程式，則會用到這很有用的公式。參閱拉普拉斯-龍格-冷次向量。
標度因子
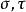拋物柱面坐標系拋物柱面坐標 的標度因子相等；而 z的標度因子是 1 ：
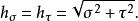拋物柱面坐標系
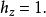拋物柱面坐標系無窮小體積元素是
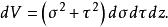拋物柱面坐標系拉普拉斯運算元是
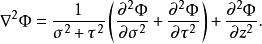拋物柱面坐標系
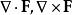拋物柱面坐標系 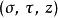拋物柱面坐標系其它微分運算元，像，都可以用坐標表示，只要將標度因子代入在正交坐標系條目內對應的一般公式。
套用
拋物柱面坐標有一個經典的套用，這是在解析像拉普拉斯方程或亥姆霍茲方程這類的偏微分方程式。在這些方程式里，拋物柱面坐標允許分離變數法的使用。
