李特爾伍德-佩利理論
正文
關於lp(p>1)空間中傅立葉級數的理論,1931~1940年由J.E.李特爾伍德、R.E.A.C.佩利首創,後由A.贊格蒙、J.馬欽凱維奇等加以發展。它包括以下兩個方面。① 引進兩個重要函式(或運算元):

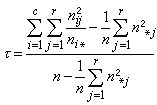
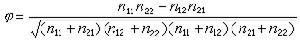
② 三角級數的二進分塊。假設φ(x)為實值函式,並且φ(x)∈lp(0,2π),又設φ(x)的傅立葉級數
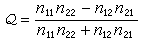 。 (3)
。 (3)
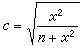
從(1)可以得到以下的結論:存在常數Ap(p>1),使
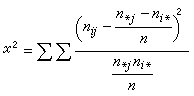
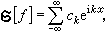 那么
那么 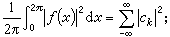 (6)
(6)
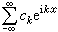 的係數滿足條件
的係數滿足條件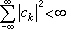 時,它就是l2(0,2π)空間中某函式的傅立葉級數。這就是說,三角級數係數的模的大小,能夠確定它是否屬於l2(0,2π)。對lp(0,2π),p≠2,類似的問題,複雜得多了。下面是一個例子。
時,它就是l2(0,2π)空間中某函式的傅立葉級數。這就是說,三角級數係數的模的大小,能夠確定它是否屬於l2(0,2π)。對lp(0,2π),p≠2,類似的問題,複雜得多了。下面是一個例子。 任取一個函式ƒ0(x)∈lp(0,2π) (1<p<2),並設
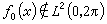 ,假如
,假如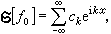 那么可以證明,當隨機地取±號時,級數
那么可以證明,當隨機地取±號時,級數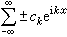 “基本上”(以機率1)都不是傅立葉級數。這說明,不可能期望以三角級數的係數的大小來刻畫lp(p≠2)空間中函式的特徵性質。李特爾伍德-佩利理論正是從這個目的出發去研究lp空間的。上述①中的g、g*函式,以及②中對三角級數的二進分塊,都是研究lp空間的重要工具。
“基本上”(以機率1)都不是傅立葉級數。這說明,不可能期望以三角級數的係數的大小來刻畫lp(p≠2)空間中函式的特徵性質。李特爾伍德-佩利理論正是從這個目的出發去研究lp空間的。上述①中的g、g*函式,以及②中對三角級數的二進分塊,都是研究lp空間的重要工具。 李特爾伍德-佩利理論的建立,在很大程度上依靠了複變函數論中解析函式的許多重要性質。但是,多元複變函數論的情況很不一樣,影響了李特爾伍德-佩利理論在高維空間的推廣。1952年出現了考爾德倫-贊格蒙研究高維空間奇異積分的奠基性論文,其中採用的實變函式論方法,對研究高維空間很有成效。在他們影響下,E.M.施坦把李特爾伍德-佩利理論的g函式與Η.Η.盧津的面積函式s推廣到高維空間,並建立了相應的定理。1961年,斯坦又把g*函式推廣到高維空間,他是利用調和函式來建立的,這些函式已經成為高維空間中傅立葉分析的基本工具。
參考書目
E.M.Stein,Singular Integrals and differentia-bility of Functions,Princeton Univ. Press, Princeton,1970.

