概念
有限測度子集定理(theorem of sets of finitemeasure)是分形幾何的一個重要定理。它有許多套用。該定理斷言：若E⊂R 為閉集，H (E)=∞，則存在緊集F⊂E，使得0<H (F)<∞。有限測度子集定理是由伯西柯維奇(Besicovitch，A.S.)於1952年獲得的。
分形幾何
分形幾何亦稱分形分析。是研究自然科學各個領域中出現的大量不規則幾何形體的新興科學，它在數學、物理、地質、材料、生命科學和工程技術等學科中有著廣泛的套用。自20世紀80年代以來，分形幾何的理論研究和實際套用迅速發展，優秀成果不斷出現，使得它不僅成為數學科學的一個非常活躍的分支，而且更成為前沿科學——非線性科學的一個重要組成部分。
自然界出現的諸如雲層的邊界，山脈的輪廓，雪花，海岸線等“不規則”幾何形體，難以用經典幾何中的直線、光滑曲面來描述。同時，大量不同類型的不規則幾何對象常常出現在自然科學的不同領域中，如數學中解決非線性問題時出現的奇怪吸引子，流體力學中的湍流，物理中臨界現象與相變，化學中酶與蛋白質的構造，生物學中細胞的生長，工程技術中的信號處理、噪聲分析……長期以來，人們試圖將它們納入經典幾何框架中進行研究，但人們發現，由此導出的模型即使在近似的情形，無論在理論上還是在實驗中，都難以處理所接觸到的實際情形.另一方面，人們已注意到不規則圖形往往能提供許多自然現象更好的描述。20世紀80年代初，由芒德布羅(Mandelbrot，B.)所創立的分形幾何，提供了研究這類不規則幾何對象的新思想、新概念、新方法和新技巧。近幾年來，這一新興學科在數學、物理、化學、地質、材料、生命科學、工程技術等諸學科中已得到廣泛套用。同時，不同學科中提出的大量問題又激勵了分形幾何的深入發展。特別應當指出的是，分形幾何的誕生與發展對整個科學的發展有極為重要的意義，誠如斯來辛格(Shlesinger，M.F.)於1986年所指出的：“20世紀的後半期似乎是科學與數學變得更加專門化的時期，令人注目的是，在前一個十年，下述兩項課題使上述趨勢得以逆轉：非線性動力學與分形。前者涉及運動的非線性確定方程的一般普適行為，而後者則是研究自相似或自仿射對象的幾何以及該幾何上的動力學。兩者均已套用到一系列深刻的交叉學科的問題中。”
自20世紀80年代後期以來，分形幾何及其相關領域取得了非常豐富的成果，特別是在自相似集性質的研究、自仿集的維數估計、2階密度、自相似測度的傅立葉分析、分形的李普希茨等價、一些特殊集的分形結構、重分形測度分析以及測度的分形理論等方面，成果更為豐碩。
另一方面，分形物理也獲得巨大進展，特別是研究在分形上(尤其是在分形晶格上)呈現的物理現象和物理性質、分形結構形成的物理機制(即探討分形形成的物理起源)方面，成果卓著。例如：分形晶格上的磁相變和臨界動力學(即臨界點附近的非平衡統計問題)、反常動力學(晶格振動、無規行走、自旋波等)、緊束縛型哈密頓量的量子力學、各種系統的多重分形研究、廣延耗散系統的自組織臨界性等；後者則包括：各種計算機模型(擴散置限聚積模型(DLA)、介質電擊模型(DBM)、解釋分形生長的理論(不動點變換、分支生長、生長界面動力學(KPZ理論)、2維拉普拉斯生長映射的哈密頓動力學等)。
大數學家黎曼(Riemann，(G.F.)B.)早在19世紀就預言過：“在很大尺度或很小尺度下，人們所遇到的幾何學可能與普通的歐幾里得幾何有很大的不同”。在大尺度方面，愛因斯坦(Einstein，A.)的引力理論提供了彎曲的時空模型，在小尺度時，情況會如何?分形幾何是否會部分地滿足上述需求?科學家們期盼著分形幾何能給出滿意的答案。
測度
測度是抽象測度的簡稱，即非負可列可加的集函式，測度論研究的對象。設μ是集類C上的擴充實值集函式，滿足下列條件：
1.若∅∈C，則μ(∅)=0;
2.μ為非負的，即對任意A∈C，有：
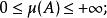有限測度子集定理3.μ為可列可加的，即對任意一列互不相交的A∈C(n=1，2，…)，且：
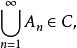有限測度子集定理有：
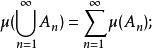有限測度子集定理則μ稱為C上的測度。特別地，當集類C為半環(環、代數、σ代數)時，μ為半環(環、代數、σ代數)上的測度。設μ為C上的測度.若對每個A∈C，均有μ(A)<+∞，則稱μ為集類C上的有限測度。若對每個A∈C，存在A∈C(n=1，2，…)，使得：
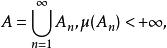有限測度子集定理則稱μ為集類C上的σ有限測度。抽象測度可看做勒貝格測度的推廣，但一般不再有面積、體積等幾何意義。在不致混淆時，帶符號的測度、向量值測度等也簡稱測度。
