發展歷史
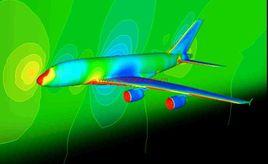
將結構用格線劃分為計算模型的一種結構分析數值方法。經過推廣發展,已成為解數學物理方程的一種近似方法。用經典結構力學進行飛行器強度計算時,需採用各種簡化和假設,把未知數的數量儘可能地減少。例如,力矩分配法能夠疊代計算含有幾個未知數的連續梁和構架,曾是一種較好的計算方法。但對於形狀、邊界條件、載荷條件複雜的結構,經典結構力學無法進行精確的計算分析。電子計算機問世後,從事飛行器結構分析的專家致力於尋求一種利用電子計算機進行結構分析的有效方法。1956年,美國波音飛機公司的M.J.脫納等人,為了分析後掠機翼研究出有限元素法。這一方法特別適合於電子計算機的套用,能對飛行器結構進行大規模的整體分析,也能對形狀複雜的結構如接頭等進行細節分析。在飛行器結構分析中,無論是靜強度分析、動強度分析、疲勞與斷裂或熱強度分析,都離不開有限元素法。它已成為一種常規的分析方法。
在有限元素法中,用格線將結構劃分為若干小塊,這些小塊稱為有限元素,簡稱有限元。它們可以是三角形、四邊形、四面體、六面體或其他形狀,易於為計算機記錄和鑑別。然後採用分片的連續函式(通常是多項式函式)來描述各元素內的位移場或應力場,並通過每個元素邊界上事先規定的一組節點與周圍元素相連線,保證必要的連續條件。以節點的廣義位移為未知數的稱位移法,未知數為廣義應力的稱力法。兩者兼而有之的是混合法。此外,在元素內假設位移場(或應力場)、而在邊界上假設應力場(或位移場)的稱雜交法。然後套用變分原理得到代數方程組,不同形式的方程組代表不同的結構分析問題。再運用各種數值解法,即可求得所需的結果。例如,用有限元素法作靜力分析,能確定結構的位移和應力;作動力分析則能求出結構的振動頻率和模態等。有限元素法廣泛套用矩陣代數,既緊湊,又易於在電子計算機上組織計算,實現計算過程標準化,可編制通用的計算程式。
有限元素法已成功地用於“阿波羅”號登月飛船、波音747旅客機等大型複雜的飛行器結構分析。除了線彈性問題外,它在彈塑性、穩定性、大變形、粘彈性、熱應力、蠕變、振動、動力回響、斷裂、疲勞裂紋擴展、溫度場、油箱晃動、噪聲回響和顫振分析等方面的套用都有很大的進展。特別是以有限元素法為基礎的結構分析系統,使分析工作具有很高的效率和可靠性。有限元素法能為新的飛行器設計提供大部分強度資料,為適航性考核和新機驗收提供依據。但對飛行器結構分析中許多複雜的非線性問題、瞬態問題、疲勞和斷裂、結構與其他介質相互作用等邊緣問題還有待進一步研究解決。
方法簡述
下面扼要敘述有限元法的整個過程:
步驟1:結構的離散化。有限元法的第一步,是把結構或連續體分割成許多單元,因而在著手分析時,必須用適當的有限元素把結構模型化,並確定單元的數量、類型、大小和布置。
步驟2:從區域或結構中取出其中一個單元來研究。選擇適當的插值模式或位移模式近似地描述單元的位移場。由於在任意給定的荷載作用下,複雜結構的位移解不可能預先準確地知道。因此,通常把差值模式取為多項式形式。從計算的觀點看多項式簡單,而且滿足一定的收斂要求,單元位移函式用多項式來近似後,問題就轉化為如何求出節點位移,節點位移確定後,位移場也就確定了。
步驟3:單元剛度矩陣和荷載向量的推導,根據假設的位移模式,利用平衡條件或適當的變分原理就可以推導出單元的剛度矩陣和荷載向量。
步驟4:由集合單元方程得到總的平衡方程組。連續體或結構由許多有限元的單元組合而成。因此,對整個連續體或結構進行有限元分析時,就需進行組合。
有限元素法與有限差分法
有限元素法實際上是基於數學上的變分原理 ,這兩種方法在處理物理問題的求解時,在處理問題的數學方法上有較大的差別。 有限差分法和有限元素法在對區域的離散化方法上也有明顯差別。有限元素法的節點配置比較任意,計算格式就要複雜得多。但這並不會影響它的實際套用。 有限差分法則是孤立地對微分方程及定解條件分別列差分方程,因而各節點精度總體上不夠一致。 有限元素法要求的計算機記憶體量比較大。 有限差分法的適用範圍要比有限元素法廣泛得多。有很多物理問題不能用有限元素法求解,但總是可以採用有限差分法。
基本原理
有限元素法也是求解邊值問題的一種數值方法。這種方法首先在20世紀40年代提出,在20世紀50年代開始用於飛機設計。後來,該方法得到了發展,並被廣泛套用於很多學科領域中,特別是現代數字計算機的迅速發展和性能不斷提高,更為有限元素法的套用和發展提供了充分的條件。
有限元素法求解的基本原理是,首先將邊值問題轉化為相應的變分問題即泛函極值問題,然後用許多子域來代表求解的連續區域。在每個子域中,未知函式用帶有未知係數的簡單插值函式來表示。這樣,整個求解區域的解就用有限數目的未知係數來近似,然後將其歸結為一個代數方程組。最後,通過求解方程組得到邊值問題的解。因此,邊值問題的有限元分析包括下列基本步驟:①求解區域的離散或子域劃分;②插值函式的選取;③方程組的建立;④方程組的求解。