有界列

有界列是一種特殊的序列。對於數列xn，若存在實數M(m)，使對所有n∈N，有xn≤M(xn≥m)，則稱xn有上（下）界。既有上界又有下界的數列稱為有界數列，簡稱有界列。

簡介

有界列是一種特殊的序列。

對於數列{x}，若存在實數M(m)，使對所有n∈N，有x≤M(x≥m)，則稱{x}有上（下）界。既有上界又有下界的數列稱為有界數列，簡稱有界列。

性質

收斂數列必有界，但有界數列不一定收斂。

當數列單調時，其有界性與收斂性是等價的。

推廣

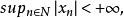有界列

對R 中的點列{x}，可類似地定義其有界性：即若存在M>0，使對所有n∈N，有|x|≤M，即這裡|·|表示歐幾里得範數。

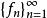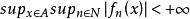有界列

有界列

對定義在A上的函式列，有兩種有界性。一種是逐點有界，指對每個x∈A，{f(x)}是有界列；另一種是一致有界，指，即存在M>0，使對所有n∈N及所有x∈A，有{f(x)}≤M，這樣的M稱為一致界。

示例

有界數列：

①1，2，3，4

②{1/n}，n=1，2，3...

無界數列：

1，2，3，4，5，6...

sin1,sin2+2……