無界列

無界列是非有界的序列，有無窮極限的數列必無界，反之不一定，但無界的單調數列必有無窮極限。

簡介

無界列

無界列

無界列是非有界的序列，R 中的點列 無界，若且唯若對任意M>0，存在正整數n，使|x|>M，即 。

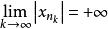無界列

無界列

這時有子列 ，使 。當m=1時就是無界數列。

性質

無界列

的實數列{x}稱為無上（下）界的數列，{x}無上（下）界，若且唯若它有子列發散於+∞（-∞）。

有無窮極限的數列必無界，反之不一定，但無界的單調數列必有無窮極限。

有界列

有界列是一種特殊的序列。

對於數列{x}，若存在實數M(m)，使對所有n∈N，有x≤M(x≥m)，則稱{x}有上（下）界。既有上界又有下界的數列稱為有界數列，簡稱有界列。

收斂數列必有界，但有界數列不一定收斂。當數列單調時，其有界性與收斂性是等價的。