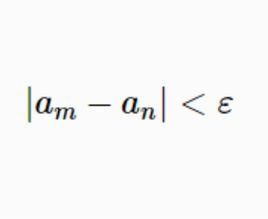基本概念
設{a}是一實數列，對任意給定的ε>0，若存在N∈N*，使得當m,n∈N*且m,n>N時，有
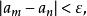基本列則稱數列{a}是一個 基本列或 Cauchy(柯西，1789~1857) 列。
粗略地說，基本列的特徵是:只要數列中兩個項充分地靠後，而不論它們的相對位置如何，它們之差的絕對值便可以小到事先任意給定的程度。
在定義中，顯然只需考慮m>n的情形。我們可以令m=n+p，這樣一來，基本列的定義可以等價地敘述為：對任意給定的ε>0，若存在N∈N*，使得當n>N時，
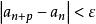基本列對一切p∈N*成立，則數列{a}叫作 基本列 。
相關性質定理
下面中心的議題是要證明：一個數列是收斂數列的充分必要條件是，它是基本列。為此，我們需做一些預備工作 。
引理1 從任一數列中必可取出一個單調子列。
證明 先引人一個定義：如果數列中的一項大於這個項之後的所有各項，則稱這一項是一個“龍頭”。分兩種情況來討論.
情況(a)如果在數列中存在著無窮多個“龍頭”,那么把這些可作“龍頭”的項依次取下來，顯然將得到一個嚴格遞減的數列.
基本列 基本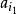列
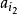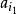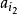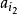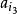基本列 基本列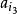 基本列 基本列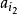
基本列 基本列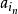 基本列
基本列情況(b) 設在此數列中只有有限多個項可作“龍頭”.這時取出最後一個“龍頭”的下一項,記作.由於不是“龍頭”,在它的後邊必有一項(i₂>i₁)滿足≤;因也不是“龍頭”,在它的後邊也必可找到一項(i₃>i₂),使得≥.如此進行下去,就得到子列{},它顯然是一個遞增的子列。
定理1(列緊性定理) 從任何有界的數列中必可選出一一個收斂的子列。
此定理也稱作Bolzano(波爾查諾,1781~1848)- Weierstrass(魏爾斯特拉斯，1815~1897)定理。
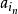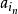基本列 基本列證明 設{a}是一個有界的數列.根據引理1，從中可以取出一個單調子列{}，這個子列當然也是有界的。易知{}是一個收斂數列。
現在來證明本節的主要定理。
定理2 一個數列收斂的充分必要條件是，它是基本列 。
證明 必要性。設{a}是一個收斂數列，其極限記作a。因此，對任意給定的ε>0，存在正整數N,當n>N時,有
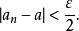基本列當m,n∈N*,且m,n>N時，可得
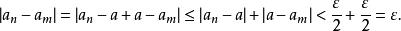基本列表明{a}是一個基本列.
充分性。設{a}是一個基本列，首先證明基本列必是有界的，對ε=1而言,可以取出一個N∈N*,且當n>N時,有
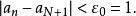基本列由此知
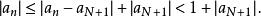基本列再令
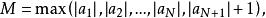基本列可見|a|≤M對一切n∈N*成立，因此，{a}是有界數列。
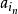基本列 基本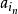列
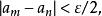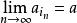基本列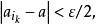
基本列
基本列根據定理1，從有界數列{a}中可選出一個收斂的子列{}，設→a (n→∞)。我們來證明這個a也是數列{a}的極限。由於{a}是基本列，對任給的ε>0,存在一個N₁∈N*,使得當m，n>N₁時，都有又因,對任給的ε>0,存在N∈N*,當k>N時，現取N= max(N₁,N₂),當n>N時，有
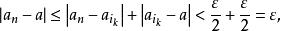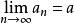基本列
基本列這正說明。
定理2又稱為數列的 Cauchy收斂原理，是一個在理論上非常重要的定理，在數學分析的全部內容中，有著各式各樣的表述，它告訴我們，當我們來判斷一個數列是否收斂時，只需通過數列的自身，而無須求助於另外的數，還應指出的是，Bolzano- Weierstrass定理和Cauchy收斂原理是實數系統連續性的另外兩種表現形式 。
