含義
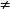 異方差性
異方差性回歸模型的隨機擾動項ui在不同的觀測值中的方差不等於一個常數,Var(ui)= 常數(i=1,2,…,n),或者Var(ui )
Var(uj )(i j=1,2,…,n),這時我們就稱隨機擾動項ui具有異方差性(Heteroskedasticity)。
在實際經濟問題中,隨機擾動項ui往往是異方差的,但主要在截面數據分析中出現。
例如
(1)調查不同規模公司的利潤,發現大公司的利潤波動幅度比小公司的利潤波動幅度大;
(2)分析家庭支出時發現高收入家庭支出變化比低收入家庭支出變化大。
在分析家庭支出模型時,我們會發現高收入家庭通常比低收入家庭對某些商品支出有更大的方差;圖5-1顯示了一元線性回歸中隨機變數的方差ui隨著解釋變數 的增加而變化的情況。
異方差性破壞了古典模型的基本假定,如果我們直接套用最小二乘法估計回歸模型,將得不到準確、有效的結果。
來源
1.模型中缺少某些解釋變數,從而隨機擾動項產生系統模式
由於隨機擾動項ui包含了所有無法用解釋變數表示的各種因素對被解釋變數的影響,即模型中略去的經濟變數對被解釋變數的影響。如果其中被略去的某一因素或某些因素隨著解釋變數觀測值的不同而對被解釋變數產生不同的影響,就會使ui產生異方差性。
例如,以某一時間截面上不同收入家庭的數據為樣本,研究家庭對某一消費品(如服裝、食品等)的需求,設其模型為:
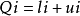 異方差性
異方差性(5-1)
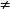 異方差性
異方差性其中Qi表示對某一消費品的需求量,Ii為家庭收入,ui為隨機擾動項。ui包括除家庭收入外其他因素對Qi的影響。如:消費習慣、偏好、季節、氣候等因素,ui的方差就表示這些因素的影響可能使得Qi偏離均值的程度。在氣候異常時,高收入家庭就會拿出較多的錢來購買衣服,而低收入的家庭購買衣服的支出就很有限,這時對於不同的收入水平Ii,Qi偏離均值的程度是不同的,Var(ui)
常數,於是就存在異方差性了。
再比如,以某一時間截面上不同地區的數據為樣本,研究某行業的產出隨投入要素的變化而變化的關係,建立如下模型:
(5-2)
其中Yi表示某行業的產出水平。Li表示勞動力對產出的影響。Ki表示資本對產出的影響,ui表示除勞動力和資本外其他因素對產出水平的影響,諸如地理位置、國家政策等。顯然,對於不同的行業 ,這些因素對產出 的影響程度是不 同的,引起 偏離零均值的程度也是不同的,這就出現了異方差。
異方差性容易出現在截面數據中,這是因為在截面數據中通常涉及某一確定時點上的總體單位。比如個別的消費者及其家庭、不同行業或者農村、城鎮等區域的劃分,這些單位各自有不同的規模或水平,一般情況下用截面數據作樣本時出現異方差性的可能性較大。
2.測量誤差
測量誤差對異方差性的作用主要表現在兩個方面:一方面,測量誤差常常在一定時間內逐漸積累,誤差趨於增加,如解釋變數X越大,測量誤差就會趨於增大;另一方面,測量誤差可能隨時間變化而變化,如抽樣技術或收集資料方法的改進就會使測量誤差減少。所以測量誤差引起的異方差性一般都存在於時間序列中。
例如,研究某人在一定時期內學習打字時打字差錯數Yt與練習打字時間Xt之間的關係。顯然在打字練習中隨時間的增加,打字差錯數將減少,即隨著Xt的增加Yt將減小。這時Var(ut)將隨Xt的增加而減少,於是存在異方差性。
不僅在時間序列上容易出現異方差性,利用平均數作為樣本數據也容易出現異方差性。因為許多經濟變數之間的關係都服從常態分配,例如不同收入組的人數隨收入的增加是常態分配,即收入較高和較低的人是少數的,大部分人的收入居於較高和較低之間,在以不同收入組的人均數據作為樣本時,由於每組中的人數不同,觀測誤差也不同,一般來說,人數多的收入組的人均數據較人數少的收入組的人均數據具有較高的準確性,即Var(ui)隨收入Ii呈現先降後升的趨勢,這也存在著異方差性。
3.模型函式形式設定不正確
模型函式形式的設定誤差。如將指數曲線模型誤設成了線性模型,則誤差有增大的趨勢。
4.異常值的出現
隨機因素的影響,如政策變動、自然災害、金融危機、戰爭和季節等。
類型
異方差一般可歸結為三種類型:
(1)單調遞增型:隨X的增大而增大,即在X與Y的散點圖中,表現為隨著X值的增大Y值的波動越來越大
(2)單調遞減型:隨X的增大而減小,即在X與Y的散點圖中,表現為隨著X值的增大Y值的波動越來越小
(3)複雜型:與X的變化呈複雜形式,即在X與Y的散點圖中,表現為隨著X值的增大Y值的波動複雜多變沒有系統關係。
檢驗存在的方法
事實也證明,實際經濟問題中經常會出現異方差性,這將影響回顧模型的估計、檢驗和套用。因此在建立計量經濟模型時應檢驗模型是否存在異方差性。關於異方差性檢驗的方法大致如下:圖示檢驗法、Goldfeld - Quandt 檢驗法、White檢驗法、Park檢驗法和Gleiser檢驗法。
1)圖示檢驗法。①相關圖分析。方差為隨機變數的離散程度,通過觀察y和x的相關圖,可以觀察的離散程度和解釋變數之間的相關關係。若隨x的增加,y的離散程度呈逐漸增加或減少的趨勢則表明模型存在著遞增或者遞減的異方差性。②殘差圖分析。通過對模型殘差分布的觀察,如果分布的離散程度有明顯擴大的趨勢,則表明存在異方差性。圖示檢驗法只能較簡單粗略判斷模型是否存在著異方差性。
2)Goldfeld - Quandt 檢驗法。將解釋變數排序,分成兩個部分利用樣本1 和樣本2 分別建立回歸模型,並求出各自殘差平方 和,若誤差項的離散程度相同,則 和 的值大致相同,若兩者之間存在顯著差異,則表明存在差異性。為在檢驗過程中“誇大”差異性,在樣本中去掉c 個樣本數據(c= n/4),則構造F統計量
對於給定顯著水平,若,則表明模型存在異方差性,反之,則不存在。
3)懷特(white) 檢驗。White 檢驗是通過建立輔助回歸模型的方法來判斷異方差性。假設回歸模型為二元線性回歸模型 則White 檢驗的步驟為:估計回歸模型,計算殘差;估計輔助回歸模型:即將殘差平方關於解釋變數的一次項,二次項和交叉乘積項進行回歸;計算輔助回歸模型的判斷係數,可以證明在同方差的假定下( ) ,其中q 為輔助回歸模型中自變數的個數:給定顯著水平,若 ,則認為至少有一個不為0( ),存在異方差性。
4)帕克檢驗( Park test ) 和格里奇檢驗( Glejsertest)。通過建立殘差序列對解釋變數的輔助回歸模型,判斷隨機項的誤差和解釋變數之間是否有較強的相關關係,以此來判斷模型是否存在異方差性。
Park檢驗:或 ;
Glejser檢驗:h=±1,±2,±1/2,……,其中 是隨機誤差項,給定顯著水平,若
經檢驗其中的某個輔助回歸方程是顯著的,則證明原模型存在異方差性。帕克檢驗和格里瑟檢驗可以判斷模型是否存在異方差,而且可以探究模型異方差性的具體形式,這為後來解決異方差性打下基礎
後果
在古典回歸模型的假定下,普通最小二乘估計量是線性、無偏、有效估計量,即在所有無偏估量中,最小二乘估計量具有最小方差性——它是有效估計量。如果在其他假定不變的條件下,允許隨機擾動項ui存在異方差性,即ui的方差隨觀測值的變化而變化,這就違背了最小二乘法估計的高斯——馬爾柯夫假設,這時如果繼續使用最小二乘法對參數進行估計,就會產生以下後果:
1.參數估計量仍然是線性無偏的,但不是有效的
2.異方差模型中的方差不再具有最小方差性
3.t檢驗失去作用
4.模型的預測作用遭到破壞
補救措施:
對模型變換,當可以確定異方差 的具體形式時,將模型作適當變換有可能消除或減輕異方差的影響。
加權最小二乘法,對原模型變換的方法與加權二乘法實際上是等價的,可以消除異方差。
買模型的對數變換,運用對數變換能使測定變數值的尺度縮小。它可以將兩個數值之間原來10倍的差異縮小到只有2倍的差異。其次,經過對數變換後的線性模型,其殘差e表示相對誤差,而相對誤差往往比絕對誤差有較小的差異。

