基本概念
偏差
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式若 , ,則稱 為 與 在[a,b]上的偏差。
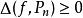 最佳一致逼近多項式
最佳一致逼近多項式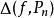 最佳一致逼近多項式
最佳一致逼近多項式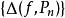 最佳一致逼近多項式
最佳一致逼近多項式註: , 的全體組成一個集合,記作: ,它有下界0。
最小偏差
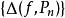 最佳一致逼近多項式
最佳一致逼近多項式若記集合 的下確界為:
 最佳一致逼近多項式
最佳一致逼近多項式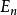 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式則稱 為 在 上的最小偏差。
偏差點
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式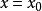 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式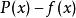 最佳一致逼近多項式
最佳一致逼近多項式設 , ,若在 上有 ,則稱 是 的偏差點。
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式若 ,則稱 是“正”的偏差點。
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式若 ,則稱 是“負”的偏差點。
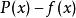 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式註:由 在 上的連續性可知,偏差點一定存在。
交錯點組
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式若函式 在其定義域的某一區間 上存在 n 個點 ,使得:
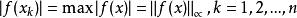 最佳一致逼近多項式
最佳一致逼近多項式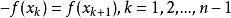 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式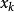 最佳一致逼近多項式
最佳一致逼近多項式則稱點集 為函式 在區間 上的一個交錯點組,點 為交錯點。
多項式
 最佳一致逼近多項式
最佳一致逼近多項式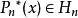 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式假定 ,若存在 使 則稱 是 在 上的最佳一致逼近多項式或最小偏差逼近多項式。
 最佳一致逼近多項式
最佳一致逼近多項式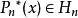 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式定理1:若 ,則總存在 ,使得
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式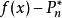 最佳一致逼近多項式
最佳一致逼近多項式定理2:設 是區間 上的連續函式, 是 的 次最佳一致逼近多項式,則 必須同時存在正負偏差點。
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式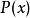 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式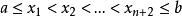 最佳一致逼近多項式
最佳一致逼近多項式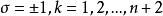 最佳一致逼近多項式
最佳一致逼近多項式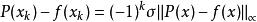 最佳一致逼近多項式
最佳一致逼近多項式定理3: 是 的最佳一致逼近多項式的充要條件是 在 上至少存在n+2個輪流為“正”、“負”的偏差點,即有n+2個,使,,這樣的點稱為Chebyshev交錯點組。
 最佳一致逼近多項式
最佳一致逼近多項式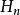 最佳一致逼近多項式
最佳一致逼近多項式推論1:如果,則在 中存在唯一的最佳一致逼近多項式
 最佳一致逼近多項式
最佳一致逼近多項式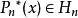 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式推論2:如果 ,則其最佳一致逼近多項式就是的一個拉格朗日插值多項式。
多項式
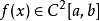 最佳一致逼近多項式
最佳一致逼近多項式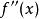 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式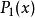 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式設,在內不變號,是 的一次最佳一致逼近多項式,則a,b屬於交錯點組。
由定理可知:
 最佳一致逼近多項式
最佳一致逼近多項式至少存在3個交錯點,
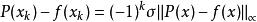 最佳一致逼近多項式
最佳一致逼近多項式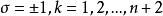 最佳一致逼近多項式
最佳一致逼近多項式,
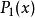 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式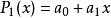 最佳一致逼近多項式
最佳一致逼近多項式因為是的一次最佳一致逼近多項式 ,所以
 最佳一致逼近多項式
最佳一致逼近多項式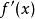 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式因為,所以 單調,所以在只有一個零點,記作,即
 最佳一致逼近多項式
最佳一致逼近多項式,另外的兩個偏差點就一定是a和b。
則有:
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式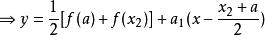 最佳一致逼近多項式
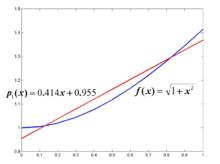
最佳一致逼近多項式幾何意義如下圖:
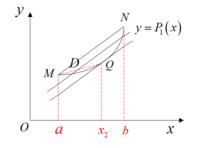 最佳一致逼近多項式
最佳一致逼近多項式例題
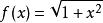 最佳一致逼近多項式
最佳一致逼近多項式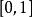 最佳一致逼近多項式
最佳一致逼近多項式求函式 在區間上的最佳一致逼近多項式。
解:
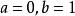 最佳一致逼近多項式
最佳一致逼近多項式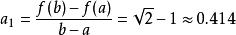 最佳一致逼近多項式
最佳一致逼近多項式,
 最佳一致逼近多項式
最佳一致逼近多項式 最佳一致逼近多項式
最佳一致逼近多項式由
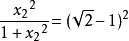 最佳一致逼近多項式
最佳一致逼近多項式得:
 最佳一致逼近多項式
最佳一致逼近多項式即:
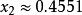 最佳一致逼近多項式
最佳一致逼近多項式解得:
 最佳一致逼近多項式
最佳一致逼近多項式故
 最佳一致逼近多項式
最佳一致逼近多項式所求一次最佳逼近多項式為
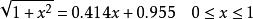 最佳一致逼近多項式
最佳一致逼近多項式故
 最佳一致逼近多項式
最佳一致逼近多項式誤差限為:
