基本介紹
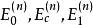最優序貫檢驗
最優序貫檢驗
最優序貫檢驗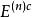
最優序貫檢驗序貫檢驗(sequential test)是指基於序貫抽樣觀測結果，運用序貫分析方法的統計假設檢驗。區分兩個統計假設H和H的序貫檢驗，在序貫抽樣觀測的每一步應採取如下三種可能行動之一： 接受H並停止觀測；接受H並停止觀測；再進行一次觀測。序貫檢驗規則可以表示為：1)對於每個n=1，2，…，將一切可能樣本值(x，…，x)的集 合劃分為三個部分 ；2)當樣本值 (X，…，X)屬於 時接受H並停止觀測，當樣本值屬於 時接受H並停止觀測；3)若樣本值屬於 ，則再進行一次觀測，取得樣本值 (X，…，X， X)，並在此基礎上重複上述步驟；4)依此類推，直到接受H或接受H為止。最優序貫檢驗是指兩類錯誤機率分別不大於給定α和β的一切序貫檢驗中，所需觀測次數(樣本容量)N的數學期望EN最小的序貫檢驗。區分兩個簡單假設的序貫似然比檢驗是最優序貫檢驗 。
序貫似然比檢驗
序貫似然比檢驗(sequential likelihood ratio test)亦稱“序貫機率比檢驗”、“沃爾德檢驗”。以似然比做統計量的序貫檢驗，是區分兩個簡單假設的最優序貫檢驗。設隨機變數X的機率函式為p(x；θ)， 關於其未知參數有兩個假設H： θ =θ和H：θ=θ，其中θ和θ是已知常數。
對於給定的兩類錯誤機率α和β，序貫似然比檢驗規則為：
1) 計算常數A= (1-β)/α和B= β/(1-α) (或α=1nA和b=1nB)；
2) 對於每個n=1，2，…，由容量為n 的簡單隨機樣本 X，…，X，計算似然比
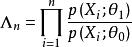最優序貫檢驗或對數似然比
3)當Λ≤B(或λ≤b)時接受H， 當Λ≥A(或λ≥α)時接受H，同時停止觀測；
4)當A<Λ<B(或α <λ<b) 時再進行一個觀測，並基於容量為n+1的簡單隨機樣本(X，…，X，X)重複上述步驟，直到最後決定接受H還是H為止 。
