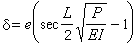柱的基本理論
正文
柱在軸向荷載作用下,由於荷載的偶然偏心,柱本身有初始彎曲,材質不均勻等原因,從載入開始時起即發生壓縮與彎曲的組合變形,即使材料遵循胡克定律,但柱的橫截面上的彎矩以及柱的側向位移(撓度)均不與荷載成線性關係。柱的性能的理論研究可按兩種不同類型的計算簡圖進行。在第一類簡圖中把柱視作本身有初始彎曲的桿或荷載有偏心的直桿,第二類簡圖則把柱視作理想中心壓桿,即認為桿是絕對直的、材料絕對均勻、荷載亦無任何偏心。有初始彎曲的桿或偏心受壓直桿 兩端鉸支的柱作為偏心受壓直桿時(圖1a)。根據小剛度桿的計算理論,任意橫截面上的彎矩為M=P(e+v),式中M為彎矩;P為荷載;e為偏心距;v為任意橫截面處桿的撓度。若桿的材料始終線上彈性範圍內工作,則由撓曲線近似微分方程EIv"=-M=-P(e+v)可得桿的中點撓度δ與荷載P有如下非線性關係:
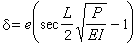
 柱的基本理論
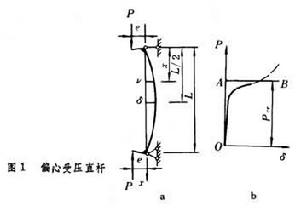
柱的基本理論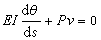 ,據此可求得P-δ曲線如圖2b中實線OABC所示。由此可知,對於理想的中心壓桿,當荷載P低於臨界值Pcr時桿保持直線形式,此時如果桿受到微小的干擾而彎曲,則干擾除去後桿即恢復原有的直線形式,即 P<Pcr時平衡的直線形式是穩定的。當P>Pcr時,理想的中心壓桿有兩種可能的平衡形式;直線形式和彎曲形式;而直線形式的平衡是不穩定的,桿在任何微小的干擾作用下發生微彎後,就會繼續彎曲直至δ達到曲線ABC上與P相對應的值。當P=Pcr時,直線OAD在A點與曲線OABC分叉,平衡是隨遇的,微小的干擾除去後桿仍保持在干擾作用時的位置上。以上分析均假設材料始終線上彈性範圍內工作。事實上,當荷載達到如圖2b中B點對應的值時,由於桿中最大應力達到彈性極限而桿所能承受的荷載迅速減小, P-δ曲線將沿虛線BE下降。這就是說,細長的理想中心壓桿所能承受的最大荷載僅稍高於臨界荷載Pcr。由於確定最大荷載需要冗長的計算,而確定臨界荷載比較簡單,所以在工程計算中,常把臨界荷載作為壓桿所能承受的最大荷載。
,據此可求得P-δ曲線如圖2b中實線OABC所示。由此可知,對於理想的中心壓桿,當荷載P低於臨界值Pcr時桿保持直線形式,此時如果桿受到微小的干擾而彎曲,則干擾除去後桿即恢復原有的直線形式,即 P<Pcr時平衡的直線形式是穩定的。當P>Pcr時,理想的中心壓桿有兩種可能的平衡形式;直線形式和彎曲形式;而直線形式的平衡是不穩定的,桿在任何微小的干擾作用下發生微彎後,就會繼續彎曲直至δ達到曲線ABC上與P相對應的值。當P=Pcr時,直線OAD在A點與曲線OABC分叉,平衡是隨遇的,微小的干擾除去後桿仍保持在干擾作用時的位置上。以上分析均假設材料始終線上彈性範圍內工作。事實上,當荷載達到如圖2b中B點對應的值時,由於桿中最大應力達到彈性極限而桿所能承受的荷載迅速減小, P-δ曲線將沿虛線BE下降。這就是說,細長的理想中心壓桿所能承受的最大荷載僅稍高於臨界荷載Pcr。由於確定最大荷載需要冗長的計算,而確定臨界荷載比較簡單,所以在工程計算中,常把臨界荷載作為壓桿所能承受的最大荷載。 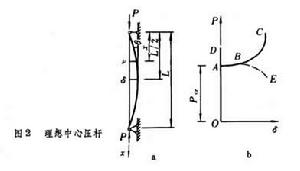 柱的基本理論
柱的基本理論Pcr=π2EI/(μL)2
式中μ為與端部約束條件有關的長度係數,μL稱為相當長度(有效長度)。將上式兩端除以柱的橫截面面積 A所得的應力,稱為歐拉臨界應力σcr=π2EI/(μL)2A=π2E/λ2
式中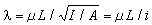 稱為柱的柔度,也稱為柱的長細比。
稱為柱的柔度,也稱為柱的長細比。 求臨界力和臨界應力的歐拉公式按其導出的條件,只適用於臨界應力σcr不超過材料的比例極限σp,即π2E/λ2≤σp的情況,也就是
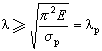 即所謂細長柱的情況。對於λ<λp的中長柱和短柱,常採用經驗公式計算臨界應力。
即所謂細長柱的情況。對於λ<λp的中長柱和短柱,常採用經驗公式計算臨界應力。 參考書目
王啟德著,林硯田等譯:《套用彈性理論》,機械工業出版社,北京, 1966。(Chi-Teh Wang, Applied Elasticity,McGraw-Hill,New York,1953.)