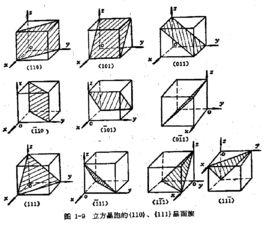
晶面和晶面族
布喇菲格子的格點，可以看成分列在相互平行、間距相等的平面繫上，而無遺漏，這些包含格點的平面稱為晶面。
因為空間格子是概括地表明晶體結構中等同點的幾何圖形，所以任何晶面必然要平行空間格子的一個格點平面。根據周期性，任何格點平面都可以經由平移操作而跟其它與之平行的格點平面作規律重複，所以在空間格子中要討論的是平行格點平面族[記為（π）]的幾何位置的數量關係而不限於一個格點平面。討論晶體結構中晶面幾何位置的數量關係時，只討論空間格子中平行格點平面族幾何位置的數量關係。因此從原子組態的晶體結構模型這個角度來談，把晶面視為由等同原子構成的平面，就可能用抽象的格點平面這種幾何平面來闡述具有物質性（原子組態）的晶面的幾何性質。但是，卻不應該將只具有抽象幾何意義的格點平面稱為晶面。
晶體多面體外形上的界面也稱為晶面，嚴格說應稱為巨觀晶面。晶體結構中的晶面可稱為微觀晶面。上述所述的晶面指微觀晶面。所謂微觀晶面應理解為與格點平面平行的等同原子的平面，不能籠統而模糊地把微觀晶面認為是晶體結構中的原子平面。實際上，晶體多面體上的巨觀晶面，可能不是一個平面而是較複雜的表面結構。在巨觀條件下不能直接觀察到界面上原子組態的結構，所看到和所感覺到的平滑晶面並不一定是平面。巨觀晶面與微觀晶面之間在原子組態結構上的連繫，必須對晶體表面結構進行實驗和理論的深入研究才能確定，不能輕易地認為巨觀晶而是與微觀晶面完全相同的等同原子平面。
空間格子平面族定理
有理係數定理
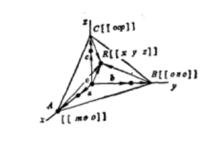示意圖在布喇菲標準定向或在以平移矢量為基矢的其它定向下，設空間格子中任何格點平面π在Ox，Oy，Oz三軸上的截矩分別為ma、nb，pc（上圖）則格點平面π的方程式為：
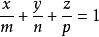晶面族式中的m，n，p三個數必是三個有理數。
定理二
晶面族
晶面族
晶面族設若晶體結構的空間格子是初基格子，則格點平面族（hkl）將基矢 a， b， c分別截成h、k、l個等分；也即是（hkl）中最靠近原點的那個格點平面在a，b，c上的截距分別是 ， ， 。
晶面和晶面族的矢量表示
天然或人工生長的晶體大多形成各種各樣多面體形狀。由於生長環境和熱力學條件的限制，這些晶體多面體常呈現不規整，很不容易看出其上晶面在空間分布的對稱性。但是，如用一球包圍著不規整的晶體多面體並從球心作各晶面的法線矢量，矢量的長皆為球半徑，則可見各晶面法線矢量的端點在球面上顯示出對稱的分布（下圖），而且在球面上測得的二矢量問的夾角的補角就是相應二晶面的面角。因此，用晶面的法線矢量來標誌該晶面的幾何位置和方位很有用處。
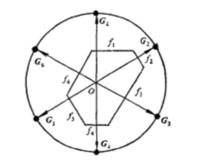用晶面法線矢量在球面上的對稱分布來顯示不規整晶體多面體的對稱在晶體結構幾何研究中除用法線矢量的方向標誌格點平面族的方位外，矢量的大小應表示平面族的某種特徵數量。
既然從晶體的原子結構模型來看可用空間格子的平行格點平面族（π）來闡明晶面的幾何性質，那末在晶體定向確定之後，一個格點平面族（π）的幾何特徵是什麼呢？格點平面族（π）的幾何特徵有二；一是其方位或取向，二是其相鄰二格點平面間的垂直距離即所謂面間距離d，如果從坐標原點引出該格點平面族的法線，此法線的方向就可唯一確定該格點平面族的方位或取向，但不能區別出取向相同而面間矩d不同的格點平面族。通常在所引法線方向作一矢量 G，取其大小等於面間距d的倒數（倒易長度），如此所取的矢量 G 就可唯一確定所考慮的格點平面族（π）（下圖）。
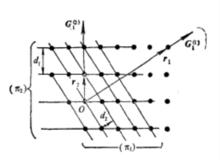標誌格點平面族的晶面基矢