晶形的分類
晶形和晶體內部構造的對稱性有關,是晶體內部構造對稱性的反映。屬於同一對稱型的晶體,可以具有完全不同的形態。實際情況下,晶體的形態更多地表現為“歪晶”,但基於面角守恆定律,通過測量和投影能恢復其理想形態。晶體的理想形態可分為單形和聚形兩大類 。
單形
單形的概念
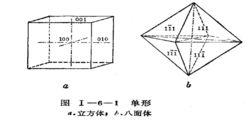 晶形
晶形單形是由對稱型中全部對稱要素聯繫起來的一組晶面的組合。或單形是指能藉助於對稱型中全部對稱要素的作用可以使它們相互重複的一組晶面 。
因此,同一單形的所有晶面彼此都是等同的。這具體表現在它們具有相同的性質,以及在理想發育的情況下晶面應是同形等大的 。
146種結晶單形
 146種結晶單形
146種結晶單形結晶單形:對稱程度各不相同的單形。
單形的推導
根據前面講的單形的概念,我們可以導出如下三條結論:
①以單形中任意一個晶面作為原始晶面,通過對稱型中全部對稱要素的作用,必可以導出該單形的全部晶面。
②在同一對稱型中,由於原始晶面與對稱要素的相對位置不同,可以導出不同的單形
③不同的對稱型可以導出不同的單形。
47種幾何單形
幾何單形:幾何形態不同的單形。有47種。它們在各晶族中的分布如圖6-13所示。
幾何單形與結晶單形數目不同,這是因為有些單形雖然幾何形態相同,但其本身的對稱性是不同的 。
單形的分類
對於上述47種幾何單形,從不同的角度出發,還可將它們劃為各種不同的類別:
1.一般形與特殊形
根據單形晶面與對稱要素的相對位置進行劃分。
特殊形:凡是單形晶面垂直或平行於任何對稱要素或者與相同的對稱要素以等角相交,則這種單形稱為特殊形。
一般形:凡單形晶面處於一般位置,即不與任何對稱要素垂直或平行,也不與相同的對稱要素以等角相交,則這種單形稱為一般形。
一個對稱型中,只可能有一種一般形。晶類即以其一般形的名稱來命名 。
 晶形
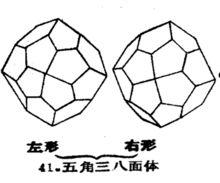
晶形2.左形與右形
互為鏡像,但不能以鏇轉操作使之重合的兩個圖形,稱為左、右形。
從幾何形態來看偏方面體、五角三四面體、五角三八面體都有左形和右形之分 。
3.正形與負形
兩個相同的單形若取向不同,但能藉助於鏇轉操作彼此重合,則兩者互為正形和負形 。
4.開形與閉形
根據單形的晶面是否可以自相閉合來劃分。開形:凡是單形的晶面不能封閉一定的空間者,例如平行雙面各種柱等。閉形:凡是晶面可以封閉一定空間者,如各種雙錐類以及等軸晶系的全部單形等 。
5.定形和變形
晶面間角度恆定的單形稱為定形,反之稱為變形。定形和變形的劃分只對幾何單形有意義 。
聚形
聚形的概念
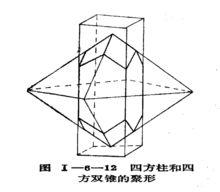 晶形
晶形有兩個或兩個以上單形按照一定對稱組合規律組合起來構成的晶體的幾何多面體便是聚形,且只有屬於同一對稱型的各種單形才能相聚。這裡的單形都是指結晶單形 。
聚形的幾何特點
1、晶面形態:在聚形中,各單形的晶面數目和晶面間的相對位置沒有變化,但由於多個單形之間的相互切割,使晶面的大小形狀與原來獨立單形相比可能會有變化。因此,在聚形中不能僅僅根據晶面形狀判斷其單形名稱 。
2、單形數目:在每一個對稱型中,可能出現的單形種數不超過7種,但在一個聚形上可能出現的單形個數是無限制的,可以有兩個或幾個同種類的單形同時存在 。
3、正形和負形的聚合:在一個聚形中可以出現指數絕對值完全對應相等而取向不同的兩個相同的單形,這時的聚形便是由一個正形和一個負形所組成 。
研究意義
對晶形的研究意義體現在兩個方面:其一,每一種礦物都有一定的晶形,可用來作辨識礦物的依據;其二,在自然界中礦物常彼此緊密結合,而不能生長出完美的晶形,因此,對晶形的研究有助於闡明礦物的成因。
如鹽的晶形是屬於正立方體形態,不過在自然界中因為常與水在一起,在晶體逐漸堆疊形成的過程中,不會完全依照正方體的堆疊模式成形,而會形成形狀各異的晶體,如雪花鹽等 。
金剛石最常見的晶形是八面體和菱形十二面體,其次是立方體和前兩種單形的聚形,晶面常成凸曲面而使晶體趨近於球形;雙晶常見;但一般以粒狀產出 。

