定義
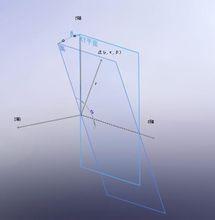
假設P點在三維空間的坐標為(x',y',θ‘)。那么|x'|是從YZ平面到P點距離,|y'|是從X軸到P點距離,0≤θ‘<2π是從X軸與P點形成的平面與XY平面的夾角。 這裡當x'=0,y'=0時,θ‘失去意義。
如用時鐘坐標系,找出P點的空間位置:
從原點往X軸移動x'單位到達P'(0,x')點。
以X軸為旋轉軸,將XY平面向外旋轉θ‘角。
從X軸上P'點在旋轉過後的平面上移動y'單位到達P點(x',y',θ‘)。
1.從原點往X軸移動x'單位到達P'(0,x')點。
2.以X軸為旋轉軸,將XY平面向外旋轉θ‘角。
3.從X軸上P'點在旋轉過後的平面上移動y'單位到達P點(x',y',θ‘)。
坐標系 變換
1.時鐘坐標系(x',y',θ‘)與笛卡爾坐標系(x,y,z)的轉換關係:
x=x'
y=y'cosθ‘
z=y'sinθ‘
2.反之,笛卡爾坐標系(x,y,z)與時鐘坐標系(x',y',θ‘)的轉換關係:
x‘=x
y‘=ysecθ'
θ‘=arctan(z/y)
3.時鐘坐標系(x',y',θ‘)與球坐標系(r,θ,φ)的轉換關係:
r=x'^2+y'^2
φ=arctg(y'cosθ‘/x')
θ=arccos(y'sinθ‘/r)
4.反之,球坐標系(x,y,z)與時鐘坐標系(x',y',θ‘)的轉換關係:
x‘=±√(r^2sinθ^2-x^2tanφ^2)
y‘=√(r^2cosθ^2+x^2tanφ^2)
θ‘=arctan(rcosθ/xtanφ)
時鐘坐標系下的微分關係
在時鐘坐標系中,沿基矢方向的三個增量元為:
dl=(dx’^2+dy’^2)^(1/2);
ds=dx'dy';
dh=y'dθ';
面積元的體積為:dS=dl*dh=(dx’^2+dy’^2)^(1/2)y’dθ'
體積元的體積為:dV=ds*dh=y’dθ'dx'dy';