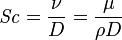簡介
施密特數(Schmidt number, Sc)是一個無量綱的標量,定義為運動黏性係數和擴散係數的比值,用來描述同時有動量擴散及質量擴散的流體,物理上與流體動力學層和質量傳遞邊界層的相對厚度有關。施密特數的命名是為了紀念德國工程師 Ernst Heinrich Wilhelm Schmidt (1892-1975)。
施密特數可定義為:
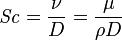 施密特數
施密特數ν 為運動黏性係數
D 為擴散係數.
μ 為動量黏性係數
ρ 為密度
分類
施密特數理論闡明物質通過兩相界面傳遞的機理的理論。主要有下列幾種:
①雙膜理論構想在兩相(例如氣-液)界面兩側分別存在著一層氣膜和液膜,膜內沒有法向流動,只有擴散。傳遞。又假設膜外的流體主體中因湍流的擴散作用而不存在濃度梯度,傳質阻力完全集中於膜內。總括氣膜傳質係數和總括液膜傳質係數。它們與膜係數和的關係如下:各傳質係數需由實驗求得,它們與設備和流體特性以及流動狀況有關。雙膜理論具有簡明的特色,多年來成功地套用於各種不相混的兩流體相系統。
②滲透理論這一理論把吸收過程看作是向半無限靜止液體中進行不穩定擴散的過程,氣相在液相中濃度的分布乃是時間的函式。這一理論的物理概念更接近於真實,算得的結果與雙膜理論的結果相差甚微。
③表面更新理論這一理論是以相界面在不斷變化、不斷更新為依據的。因而引出了“表面年齡”的概念,算得的結果與施密特數理論的結果相差很小。
湍流施密特數
湍流施密特數通常用於湍流研究,並被定義為
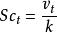 施密特數
施密特數vt是以(m2 / s)為單位的渦流粘度;
k是渦流擴散係數(m2 / s)。
湍流施密特數描述了動量的湍流傳播速率與質量(或任何被動標量)的湍流傳輸之間的比率。 這與涉及湍流傳熱而不是湍流傳質的湍流普蘭特數有關。
斯特林發動機
對於斯特林發動機,施密特號碼與特定功率有關。 布拉格德國理工學院的古斯塔夫·施密特(Gustav Schmidt)在1871年發表了一個分析,用於理想的等溫斯特林發動機模型的著名的封閉式解決方案。
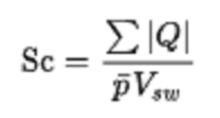 施密特數
施密特數Sc是施密特數;
Q是傳遞到工作流體中的熱量;
p是工作流體的平均壓力;
V是活塞的體積。