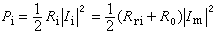正文
微觀動力學和巨觀動力學 冶金過程通常是在高溫、有多相存在和有流體流動下的物理化學過程。反應速度除了受溫度、壓力和化學組成及結構等因素的影響外,還受反應器(如冶金爐等)的形狀和物料的流動狀況以及熱源等因素的影響。當反應的條件發生變化時,反應進行的途徑(步驟)即反應機理也要發生變化。從分子理論微觀地研究反應速度和機理稱為微觀動力學。一般情況,物理化學中的化學動力學屬於微觀動力學的範疇;結合反應裝置在有流體流動、傳質及傳熱條件下巨觀地研究反應速度和機理稱為巨觀動力學。冶金過程動力學即屬於巨觀動力學的範疇。反應的控制步驟 為使某一反應進行,必須將參與反應的物質傳送到反應進行的地點(界面),在那裡發生反應,並使反應產物儘快排除。其中速度最慢的步驟限制著整個反應的速度,這個最慢的步驟稱為控制步驟或限制環節。研究反應速度的目的就是要弄清在各種條件下反應進行的各種步驟,也即反應的機理,找出它的限制環節,並導出在給定條件下反應進行的速度方程式,以便用來控制和改進實際操作。
反應速度 通常以單位時間物質i的濃度 Ci(對非理想溶液採用活度ai)的變化來表示,即反應速度表示為
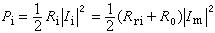 。對反應物,反應速度vi是負值;對產物則vi為正值。以不可逆反應
。對反應物,反應速度vi是負值;對產物則vi為正值。以不可逆反應 aA+bB─→cC+dD
為例,如果體系的總體積不變,則反應物減少量和產物生成量與方程式中計量比a、b、c、d 的關係為
-dCΑ∶-dCB∶dCC∶dCD =a∶b∶c∶d
用反應物(A或B)或產物(C或D)的濃度表示的反應速度的相互關係為
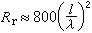
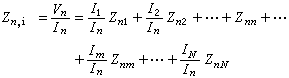
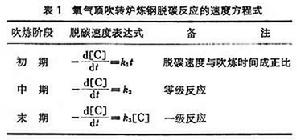
氧氣頂吹轉爐煉鋼的脫碳反應,由鋼液中的反應方程式【C】+【O】─→CO來看,似應為二級反應,但實驗表明,此反應相當複雜,其反應級數隨冶煉階段而變化(表1)。由於煉鋼過程的重要反應大部分在鋼液-熔渣界面上進行,單純研究均相反應的級數,其實際意義不大。
 冶金過程動力學
冶金過程動力學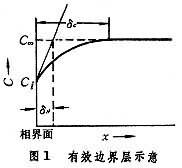 冶金過程動力學
冶金過程動力學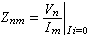 代表傳質速度, 即單位時間傳遞的物質的摩爾數(摩爾/秒);J代表傳質通量,即單位時間內通過垂直於傳質方向 (沿x)的單位面積上的物質的摩爾數[摩爾/(米2·秒)];A代表面積,顯然
代表傳質速度, 即單位時間傳遞的物質的摩爾數(摩爾/秒);J代表傳質通量,即單位時間內通過垂直於傳質方向 (沿x)的單位面積上的物質的摩爾數[摩爾/(米2·秒)];A代表面積,顯然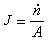 。根據斐克(Fick)第一定律:
。根據斐克(Fick)第一定律: 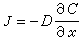
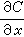 為物質沿x方向的濃度梯度(物質是沿與x相反的方向向相界面傳遞)。圖1中δσ是濃度邊界層的厚度(米或厘米),但有效濃度邊界層δ N的定義為
為物質沿x方向的濃度梯度(物質是沿與x相反的方向向相界面傳遞)。圖1中δσ是濃度邊界層的厚度(米或厘米),但有效濃度邊界層δ N的定義為 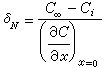
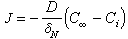
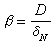
為傳質係數(米/秒或厘米/秒),1/β為物質在相界附近的傳質阻力。以上各式均按穩態,即濃度梯度不隨時間變化的情況下分析的。對非穩態則採用斐克第二定律在已知的邊界條件下求解。
② 動量傳遞。當流體沿固體平行流動,或兩個密度懸殊的液體相互流動,在相界面產生摩擦,形成速度邊界層δpr,而在相界面上的流體速度為零。研究動量傳遞則採用類似的牛頓粘滯定律。
③ 傳熱。當流動的流體接觸固體時,發生對流傳熱,流體內部的溫度不同於相界面的溫度,在固體表面附近形成一溫度邊界層δ T。 研究傳熱則採用類似的傅立葉(Fourier)定律。
三傳現象(傳質、動量傳遞及傳熱)對研究冶金過程動力學非常重要。例如在煉鐵高爐中,焦炭在風口燃燒產生大量的高溫氣體,後者沿爐身上升,而加入的爐料則自爐頂下降,在高溫區鐵滴及熔渣滴穿過焦炭流入爐缸。高爐中充滿了氣、固、液流動體,在它們的相互流動中發生熱交換及物質交換。所以研究高爐反應動力學必須研究三傳的作用。又如為提高鋼質量的噴射冶金,用氬氣將固體粉料噴入鋼液中,形成氣泡、固體顆粒及液體的流動體,這裡動量傳遞起重要作用。對連續鑄錠,用電磁攪拌研究凝固速度與鋼液流動的相互關係,從而改進鋼坯的表面質量,這裡傳熱起重要作用。
多相反應模型 雙膜理論 為了研究反應機理和控制步驟有必要設計冶金過程的模型。熔渣和金屬液的反應常用雙膜理論模型來處理(圖2)。圖內Ⅰ、Ⅱ分別代表熔渣和金屬液兩個相,CⅠ、CⅡ為某組分在Ⅰ、Ⅱ兩相內部的濃度,C 媽、C嫇為相界面處的濃度,x為距相界面的距離。從Ⅰ相內部向相界面的傳質通量JⅠ,即單位面積的傳質速度為
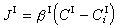
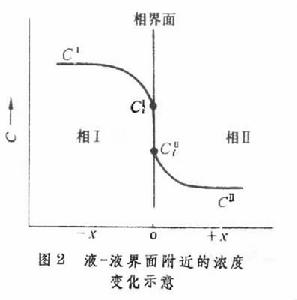 冶金過程動力學
冶金過程動力學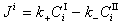
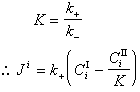
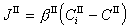
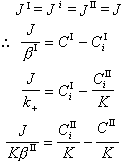
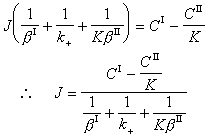
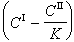 是總反應的推動力,
是總反應的推動力,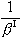 是Ⅰ相的傳質阻力,
是Ⅰ相的傳質阻力,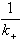 是界面反應的阻力,
是界面反應的阻力,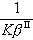 是Ⅱ相的傳質阻力。這三個阻力之和就是總反應的阻力。通常,界面反應很迅速,k+很大,則
是Ⅱ相的傳質阻力。這三個阻力之和就是總反應的阻力。通常,界面反應很迅速,k+很大,則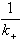 很小,可以忽略不計。傳質速度決定於某一相邊界層的擴散阻力或雙方邊界層的擴散阻力。
很小,可以忽略不計。傳質速度決定於某一相邊界層的擴散阻力或雙方邊界層的擴散阻力。 對於鋼液-熔渣反應,例如:鋼液中的Mn與溶渣中的FeO(Fe2+)反應:
【Mn】+(FeO)─→(MnO)+【Fe】
或 【Mn】+(Fe2+)─→(Mn2+)+【Fe】
其進行步驟為:
① 鋼液中Mn原子向鋼渣界面擴散移動;
② 渣中Fe2+離子向鋼渣界面擴散移動;
③ 在鋼渣界面上完成化學反應;
④ 生成的Mn2+離子從界面向渣內部擴散移動;
⑤ 生成的Fe原子從界面向鋼液內部擴散移動。
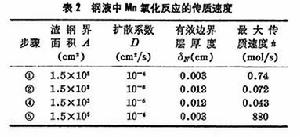
步驟③是化學反應,在高溫下反應速度很快,不可能是控制步驟。曾根據渣中含Mn2+5%、Fe2+20%,鋼液中含Mn0.2%,溫度為1600℃進行過計算(表2)。可以看出④的速度最慢,是控制步驟,它控制著[Mn]氧化入渣的整個反應。根據現有的研究成果,在煉鋼雜質去除過程中,矽、磷在鋼液中的擴散是控制步驟,而錳、硫在渣中的擴散是控制步驟。但當渣中含有大量不溶解的磷酸鈣或氧化鈣時,PO婯 離子在渣中的擴散則成為磷的氧化反應的控制步驟。提高溫度降低熔體粘度或採用攪拌(機械或氣體攪拌)均可提高傳質速度。
 冶金過程動力學
冶金過程動力學Fe3O4+4CO─→3Fe+4CO2
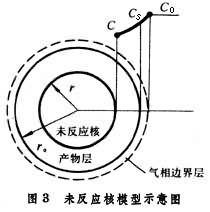
設球形試樣(如球團礦)還原時,反應區域是由表面等速向中心推進的;反應前後,球團的體積沒有變化;固態產物是多孔的;還原氣體可以通過產物層擴散(內擴散)到反應區域。當界面的化學反應按一級反應處理時,還原總反應速度為
 冶金過程動力學
冶金過程動力學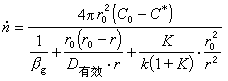
總反應速度公式右邊分母第一項代表氣體邊界層的傳質阻力,第二項代表還原氣體通過固體多孔產物層的內擴散阻力,第三項代表界面化學反應的阻力。這些阻力的相對作用大小隨著礦石的種類、性質和反應條件而變化。
未反應核的半徑r是無法直接測得的,在套用該式時常用反應的轉化率或還原度f 來代替:
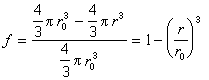
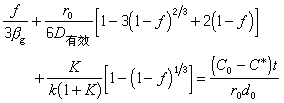
冶金過程中的鐵礦石還原,石灰石焙解等都是適用未反應核模型的氣固相反應。但由於礦石顆粒本身也有孔隙度,化學反應可能在顆粒內部任何地區進行,不一定有一明確的反應區域;而且因為這些反應經常是吸熱的,需要外來熱源,伴有傳熱現象;所以全面地分析尚需要更複雜的反應模型。
冶金過程動力學的發展概況 從分子理論研究反應速度的化學動力學自1850年開始,已有百餘年的歷史。套用於冶金過程的巨觀動力學自20世紀40年代末期開始發展。隨著氧氣頂吹轉爐煉鋼、連續鑄錠、閃速熔煉和噴射冶金等新技術的發展,冶金過程動力學已成為70年代以來頗為活躍的邊緣學科。除了用動力學理論及實驗方法研究冶金過程的反應速度和機理外,冶金過程動力學的另一個發展趨勢是向冶金反應工程學發展。
參考書目
H.Y. Sohn & M. E.Wadsworth,Rate Processes of extractive Metallurgy,Plenum,New York,1979.
J.Szekely & N.J. Themlis, Rate Phenomenɑ in Process Metallurgy,Wiley-Interscience,New York,1971.
黃希祜主編:《鋼鐵冶金原理》,第五章:冶金反應過程動力學,冶金工業出版社,北京,1980。
川合保治(日)著,徐同晏、戴嘉惠譯:《鋼鐵冶金反應動力學》,冶金工業出版社,北京,1982。(川合保治:《鉄冶金反応速度論》,日刊工業新聞社,東京,1973。)