組成部分
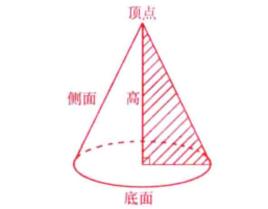
以直角三角形的一條直角邊所在的直線為軸,其餘兩邊繞軸鏇轉360°所得到的幾何體,叫做 直圓錐,簡稱 圓錐,如圖1。
直角三角形鏇轉時,有一條直角邊位於鏇轉軸上,另一條直角邊鏇轉產生的圓面叫做圓錐的底面。斜邊鏇轉時的每一個位置,叫做直圓錐的母線,鏇轉時產生的曲面叫做直圓錐的側面。斜邊位於軸上的端點叫做直圓錐的頂點。直圓錐的頂點和底面的距離(即頂點和底面圓圓心的距離)叫做直圓錐的高。
直圓錐的底面是圓。
直圓錐的側面沿母線剪開後在平面上展開,是一個扇形。它的半徑等於直角三角形的斜邊長,它的弧長等於直圓錐的底面圓的周長。圖2就是直圓錐的側面展開圖 。
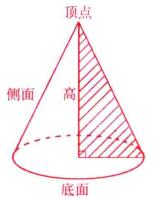 圖1
圖1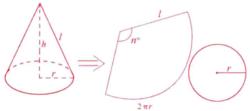 圖2
圖2性質
直圓錐的主要性質:
(1) 直圓錐的底面是個圓。它所在的平面垂直於圓的軸。
(2) 直圓錐的軸經過頂點和底面的圓心,底面圓心和頂點的連線是圓錐的高。
(3) 直圓錐的一切母線都交圓錐的頂點,並且都相等,各條母線與軸的夾角都相等。
(4) 用一個過直圓錐的頂點,並且和底面相交的平面去截直圓錐,所得的截面是一個等腰三角形。
(5) 垂直於軸的直圓錐截面是個圓。
體積與側面積
直圓錐體的體積等於它的底面積與高的積的三分之一。
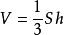 直圓錐
直圓錐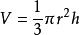 直圓錐
直圓錐若設圓錐體的體積為V,底面積為S,高為h,那么,圓錐體的體積公式為或。
直圓錐體的側面積等於它的底面的周長與母線長乘積的一半。
 直圓錐
直圓錐 直圓錐
直圓錐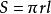 直圓錐
直圓錐若圓錐的母線為,底面半徑為,側面積為S,那么,圓錐體的側面積公式為。
方程式
由方程
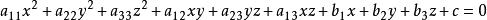 直圓錐
直圓錐給出的曲面,叫做 二次曲面。
這個方程給出的可以不是曲面,而是具有更小維度的圖形:直線,點或者甚至是空集合。這樣的圖形我們不列入二次曲面。
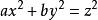 直圓錐
直圓錐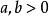 直圓錐
直圓錐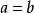 直圓錐
直圓錐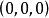 直圓錐
直圓錐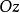 直圓錐
直圓錐二次曲面稱為 圓錐,如果在某個直角坐標系中它用方程給出,其中。在這種情況,圓錐稱為 鏇轉圓錐或者 直圓錐。點稱為圓錐的頂點,而軸叫做圓錐的軸。
相關結論
【例1】證明:頂點在坐標原點的直圓錐的方程形式為
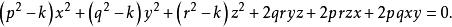 直圓錐
直圓錐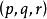 直圓錐
直圓錐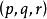 直圓錐
直圓錐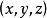 直圓錐
直圓錐證明提示:設圓錐軸的方向用向量給出,向量和之間的角的餘弦等於
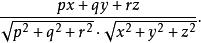 直圓錐
直圓錐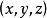 直圓錐
直圓錐點的集合,對於它這個餘弦精確到符號相同,給出方程的形式為
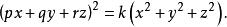 直圓錐
直圓錐【例2】證明:如果圓錐
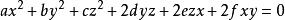 直圓錐
直圓錐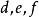 直圓錐
直圓錐是直圓錐,並且數中一個等於零,那么這些數中還有一個等於零。
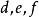 直圓錐
直圓錐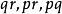 直圓錐
直圓錐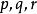 直圓錐
直圓錐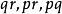 直圓錐
直圓錐證明提示:根據上一問題數具有形式。如果這些數中有一個等於零,那么由數中一個等於零,則由數中還有一個等於零。
【例3】證明:圓錐
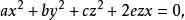 直圓錐
直圓錐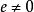 直圓錐
直圓錐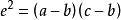 直圓錐
直圓錐其中,是直圓錐,若且唯若。
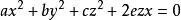 直圓錐
直圓錐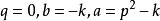 直圓錐
直圓錐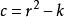 直圓錐
直圓錐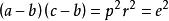 直圓錐
直圓錐證明提示: 首先假設,圓錐是直圓錐,根據問題 ①有和,所以。
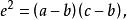 直圓錐
直圓錐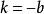 直圓錐
直圓錐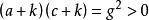 直圓錐
直圓錐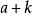 直圓錐
直圓錐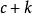 直圓錐
直圓錐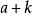 直圓錐
直圓錐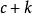 直圓錐
直圓錐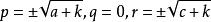 直圓錐
直圓錐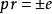 直圓錐
直圓錐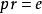 直圓錐
直圓錐現在假設設,根據條件,所以和要么兩個都正,要么兩個都負,在必要時改變圓錐方程的所有係數的符號,可以認為,數和是正的,假設,根據條件,符號可以選擇,使得成立等式,這時圓錐的方程化歸為正如在問題①指出的這樣的形式。
【 例4】直圓錐用不平行於它的軸的平面的截形,射影在垂直於圓錐的軸的平面上,證明:圓錐的軸相交射影於焦點。
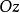 直圓錐
直圓錐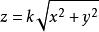 直圓錐
直圓錐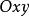 直圓錐
直圓錐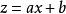 直圓錐
直圓錐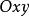 直圓錐
直圓錐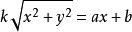 直圓錐
直圓錐證明提示:可以認為,圓錐的頂點位置在坐標原點,而它的軸沿著軸的方向,則圓錐的方程具有形式。坐標平面鏇轉後可以認為,截割平面的方程具有形式,這樣一來,圓錐截形在坐標平面上的射影由方程給出,這個方程可以改寫為
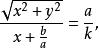 直圓錐
直圓錐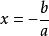 直圓錐
直圓錐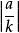 直圓錐
直圓錐最後一個方程給出焦點在坐標原點,準線為和離心率為(由點到焦點的距離對點到準線距離的比等於離心率)的二次曲線 。