基本介紹
解析幾何指出：用平面去截對稱的對頂圓錐，平面和圓錐側面相交的曲線統稱為圓錐曲線。圓錐曲線是二元二次代數方程的解析式——ax²+bxy+cy²+dx+ey+f=0的幾何化。對於任意一個二元二次方程，都有一條圓錐曲線與之對應，反之，對於任意一條圓錐曲線，也必然有一個二元二次方程作為它的解析式。圓錐曲線的變化，反映著二元二次方程的變化，反之亦然。那么圓錐曲線是怎樣變化的呢?我們分兩種情形來說明。
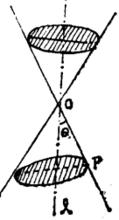圖1 對頂圓錐首先，平面經過圓錐頂點O，並且和中軸l垂直，這時其交線變為一點，若平面繞頂點逆時針旋轉，隨著旋轉的量變積累，其與原平面的二面角等於90°—θ時，平面與圓錐側面相交成為直線(即圓錐的側棱)，這便是量變引起的質變了。過了這個關節點，即二面角大於90°—θ時，其交線變為相交於圓錐頂點的兩條直線了。在這裡又是一次漸進過程的中斷——飛躍。 平面繼續旋轉直至180°時，交線的變化又依次為一條直線，一點。
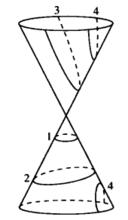圖2 對頂圓錐其次，平面不經過圓錐頂點，而與其相交於任意點P，且平面與軸l垂直，此時交線是一個圓。 平面繞P點逆時針旋轉，交線便由圓轉化為橢圓，發生了質變。隨著旋轉的量的增加，共與原平面的二面角等於90°一θ時，橢圓又質變為拋物線了。過了這個關節點，即二面角大於90°—θ時，其交線又變為雙曲線了。平面繼續旋轉並達到180°的過程中，這種量變質變又會按顛倒了的次序重演。
曲線形式(第一種情形所得各種點、線，是圓錐曲線的特例)的量變質變，表現在描述曲線的方程上，就是二次曲線方程離心率e的量變質變 。
具體情況分析
(一)、若一截面僅平行於圓錐的一條母線，則截面與圓錐面的截線為拋物線。
圖3如圖3，設有圓錐S-AB，平面γ //母線SA，交圓錐底面於MN，MN⊥AB。設P為平面γ與圓錐面截線上任一點。作圓錐S的一個內切球，內切球與圓錐面的切點圓平面為α，平面α與平面γ的交線為直線l，內切球切平面γ於F，連PF。
因平面α//圓錐底面，所以直線l//圓錐底面，所以MN//直線l，又MN⊥母線SA，所以SA⊥直線l。 過P作PC//SA，因SA//平面γ，所以PC 在平面γ內，所以PC⊥直線l。又設SA交平面α於D，連C、D交SP於E，因E在平面α內，又在圓錐母線SP上，所以E必在內切球與圓錐相切的切點圓上 。
由PC//SD，△SDE∽△PCE因SD=SE，所以PC=PE又PE、PF同為內切球的兩切線，所以PF=PE，所以PC=PF，所以P 點的軌跡是以F為焦點、以直線l為準線的拋物線。
(二)、若一截面不過圓錐頂點而與圓錐面的所有母線都相交，則截面與圓錐面的截線為橢圓。(當截面與圓錐的軸垂直時，截線為圓)
圖4如圖4，設有圓錐S-AB，平面β斜交圓錐所有母線，P為平面β與圓錐面的截線上任一點。 在圓錐內部、平面β兩側各作一內切球O₁和內切球O₂，使與圓錐側面及平面β相切，得兩個切點圓及兩切點F₁、F₂。設母線SP交內切球O₁的切點圓於C，交內切球O₂的切點圓於D，連PF₁、PF₂。因PF₁、PC同為過P點的內切球O₁的兩條切線，PF₂、 PD同為過P點內切球O₂的兩條切線，
∴PF₁= PC，PF₂= PD，PF₁+PF₂=PC+PD=CD=定長，
∴P點的軌跡是以F₁、F₂為兩焦點、以CD為長軸長的橢圓 。
(三)、若一截面不過圓錐頂點，且同時與圓錐面及其對頂圓錐面都相交，則截面與圓錐面的截線為雙曲線。(截面與兩母線平行)
圖5
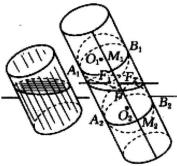圖6如圖5，設有圓錐S-AB，平面δ同時與圓錐S-AB及對頂圓錐面都相交，P為相交截線上任一點。在對頂圓錐內分別作內切球O₁、內切球O₂與圓錐面及平面δ都相切，分別得兩個切點圓及切點F₁、F₂，連PF₁、PF₂。又設母線PS分別交內切球O₁、內切球O₂於C、D。
因PF₁、PC同為過P點的內切球O₁的切線，PF₂、PD同為過P點的內切球O₂的切線，
∴PF₁= PC，PF₂=PD，
∴PF₁-PF₂= PC- PD=CD=定長，
∴P點的軌跡是以F₁、F₂為兩焦點，以CD為實軸長的雙曲線。
現在，我們也能證明為什麼球被陽光斜照後的影子是橢圓，為什麼圓柱形玻璃杯中水被傾斜後液面成橢圓。
如圖6，在圓柱內放進兩個內切球O₁和內切球O₂，使與圓柱側面及斜截面都相切，分別得切點圓O₁、切點圓O₂及兩切點F₁、F₂。設P為圓柱斜截面交線上任一點，過P作圓柱母線，交兩切點圓於M₁、M₂，
PM₁=PF₁，PM₂= PF₂，PF₁+PF₂= PM₁+ PM₂ = M₁M₂=定長，
∴P點的軌跡為以F、F為兩焦點、長軸長為M₁M₂的橢圓 。
