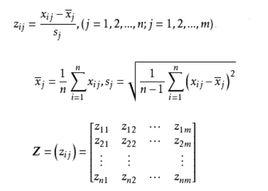基本介紹
 數據規格化
數據規格化 數據規格化
數據規格化 數據規格化
數據規格化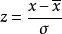 數據規格化
數據規格化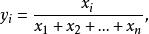 數據規格化
數據規格化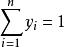 數據規格化
數據規格化有時在試驗中,每個標本(樣品)有許多種測定值。每種測定值的量綱和數量大小是很不一樣的,有的變數的絕對值很大,有的很小,變化幅度很不一樣。假如直接用原始數據進行計算,就會突出那些絕對值大的變數,而壓低絕對值小的那些變數的作用 。為 了能正確地真正反映實際情況,必須對原始數據進行加工處理,使之規範化。比如,文體競賽活動中,對於評審所打的分數(原始數據),首先去掉一個 (或兩個)最高分,一個(或兩個)最低分,然後再求其餘分數的算術平均數,以來代表被評者的最後得分, 再去和其他參賽者比較優劣。又如,對原始數據進行標準化處理也是數據規格化的例子。 設有一組數據x,x, …,x,其平均數為,標準差為σ,用公式處理後所得的數據z,z,…,z即為標準化數據。可以證明標準化數據z,z,…,z的平均數為 0,標準差為1。因此,對於各個考試科目所得的原始分數,不管平均分和標準差多么的 不同,它們一旦都化成標準分數之後,就都變成了平均數為0,標準差為1的統一固定不變的標準形式。它的大小和正負可以反映某一考分在全體考分中所處的地位。正數為上游,數值越大說明位置越靠前;負數為下游,負數的絕對值越大說明位置越靠下;零分為中游,零分左右靠近中游。將考生各科目的標準分數相加來比較總分的高低以區分考生總成績的優劣比較合理。再如,歸一化處理也是數據規格化的例子。在需要區分各個因素重要性大小的問題中,用原始數據的大小也能看出哪個因素重要,哪個因素次之,哪個因素最不重要。但是對重要程度的表述,既不精確也不規範。為此,可以進行歸一化處理: 設原始數據為x,x,…,x,歸一化處理後的相應數據為y,y,…,y。兩組數據間的關係是 式中i=1,2,…,n。可以證明: 對於任一個y,均有0<y<1且,y×100%就是第i個因素在所有因素所組成的總體中的重要程度 。又如聚類分析是根據各變數的觀測值予以分類的。它涉及到分析測試等各種手段得來的數據,而這些數據測得的量綱,量級都不盡相同,這就使運算過程中可能突出某些數量級特別大的變數對分類的作用,而壓低甚至排除了某些量級很低的變數作用。這樣對各變數的分類作用缺乏一個統一尺度。為此,在使用某些數據參加聚類分析計算前,必須對它進行必要的處理或變換,也就是所謂的施行數據規格化,以消除測量單位的分歧,並將每一變數統一於某種共同的數值特徵範圍。
規格化處理的方法
規格化處理通常的方法有數據的標準化、正規化、均值化及對數變換等 。
數據標準化
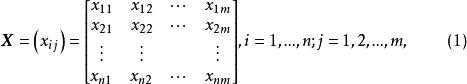 數據規格化
數據規格化 數據規格化
數據規格化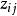 數據規格化
數據規格化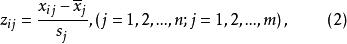 數據規格化
數據規格化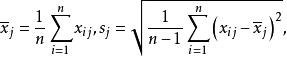 數據規格化
數據規格化 數據規格化
數據規格化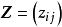 數據規格化
數據規格化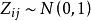 數據規格化
數據規格化設有n個樣品,每個樣品測量了m項指標(變數),得到如下原始數據矩陣: 其中,i為樣品個數,j為變數個數。表示第i個樣品第j個變數的觀測值。設變換後的數據記為,則: 其中, 寫成矩陣形式為: 則稱為為標準化數據。若所取樣品構成的變數服從常態分配,則標準化後的數據。
數據正規化
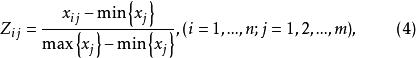 數據規格化
數據規格化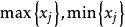 數據規格化
數據規格化 數據規格化
數據規格化所謂數據正規化,就是通過極差變換,把原始數據矩陣中的任何一列的最小值化為0,最大值化為1,其餘介於0與1之間。記: 其中,分別為第j個變數的最大值與最小值 。寫成矩陣形式為:
中心化
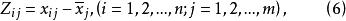 數據規格化
數據規格化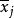 數據規格化
數據規格化的意義同上。
對數化
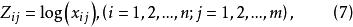 數據規格化
數據規格化極大值規格化
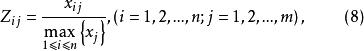 數據規格化
數據規格化新數據≤1。
均值規格化
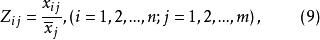 數據規格化
數據規格化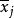 數據規格化
數據規格化的意義同上。新數據的均值為1。
標準差規格化
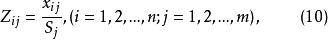 數據規格化
數據規格化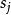 數據規格化
數據規格化的意義同上。新數據的標準差為1 。