基本概念
在一般的處理器中，浮點加法、減法、轉換和傳送最終都是可以轉換為採用浮點加法器實現，所以浮點加法器的使用頻率高達55%，是使用頻率最高的浮點運算模組。浮點加法的兩個特點，一是它複雜，二是它被使用的頻率在所有操作裡面是最高的，所以它是現代微處理器和數位訊號處理器中非常關鍵的部分。因此，浮點加法器的設計對FPU的整體性能十分重要。
浮點數的基本運算包括加法、減法、乘法和除法。目前浮點加法算法主要有基本算法、Two-Path算法和Triple-data-path算法。
浮點加法器基本算法
標準數據格式
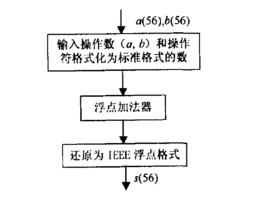
IEEE標準格式的二進制浮點加法器完成兩個二進制數相加時，要求輸入的兩個二進制數與輸出的和數均為56位，其指數(e)為8位，尾數(f)為47位，符號位(s)為1。lEEE格式的標準數如下：
浮點加法器它與普通二進制浮點數的差別是增加了2位：第47位設為尾數為‘1’的隱含位；第56位是指數為‘0’的符號擴展位。
浮點加法器的框圖
設加法運算的兩個數為：
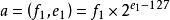浮點加法器
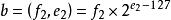浮點加法器加法運算表達式為：
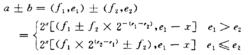浮點加法器浮點數的加（或減）運算可分3步做：
第1步：比較數據大小，以便對數據小的尾數進行移位，從而在尾數運算前完成對階的工作。
第2步：對尾數進行加（減）法運算。
第3步：對運算結果格式化，還原為IEEE浮點格式。浮點加法器框圖如圖所示 ：
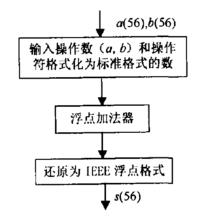浮點加法器圖1
算法設計和結構映射
浮點加法器
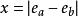浮點加法器當浮點數的格式化完成後，第1步就是用比較指數的大小，完成對階的工作。這也是整個加法器設計的核心部分。其主要作用是把運算結果作為尾數運算的條件，控制尾數運算始終由大數加（或減）小數，同時結果的符號以大數的符號作為參照。具體作法是並行地比較指數的大小，得出的值，只在x=0（階對齊）的情況下做尾數比較大小的運算，並根據x的值對小指數的尾數右移對階，最後對運算結果的指數按輸出數據的格式做相應修正，以滿足數據格式要求。
基本算法步驟
對於浮點加法操作來說，一般要求以下一系列的基本操作步驟 ：
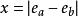浮點加法器（1）階碼相減：完成兩十運算元階碼相減，形成階差。
（2）對齊：小的操作散的有效位右移d位。
（3）有效位相加：根據攤作碼和操作散的符號完成加法或減法。
（4）轉換：當有救位的結果為負數時，轉換為符號一尾數的表示方式。因為尾數採用原碼錶示，所以轉換需要求補操作，即包括一個加法步驟。
（5）前導1的判定：判定由於減法結果產生的左移位數，對於加法判定是否右移一位或不移。對前導1判定的結果進行編碼以驅動規格化移位。
（6）規格化：規格化有效位並且根據移位的方向和位數修改大的階碼。
（7）捨入：根據IEEE標準判定對最終結果的捨入，如果需要入，則在最末有效位加1。假如捨入引起溢出，則需要有效位右移1位，同時階碼加1。
由於需要很多的部件，這個算法的延時很大。
浮點加法的Two-Path算法
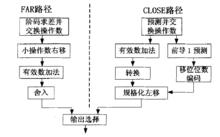
浮點加法器的設計經過多年的發展，在算法的改進上取得了大量的成果，其中最重要的就是Two-Path算法。基於這種算法的加法器已經在一些商用機上設計實現。隨後，人們在此基礎上逐步完善，使算法的性能進一步提高，並得到了更加廣泛的套用。結構圖如圖：
浮點加法器Frmwald針對浮點加法的基本算法進行了一系列的改進，提出了Two-Path算法。此算法的目的就是使各十操作步驟儘可能地並行化，以減少算法總的延時。這些改進一般都需要附加的硬體。改進是基於浮點加/減計算的某些特性。
（1）階碼差的符號決定兩個運算元哪一個大。交換運算元，使其總是大的藏小的，在所有情況下，除了階碼相等的情況外，第4步轉換將被取消。在階碼相等的情況下，第3步的結果可能是負的，僅在這種情況下需要轉換。因為不需要初始的對階移位，減後的結果是一個精確值，因此也就不需要捨入。所以遙過運算元的交換，使第4步的加法和第7步的加法互斥。這樣可以消減三個全長加法延時中的一個。
浮點加法器 浮點加法器（2）在有效的加法中．規格化移位操作是不需要的。因此，只有一個全長的對階移位。對於減法，需要區分兩種情況。第一，階差d>1，可能需要一個生長的對階移位。然而，它卻不需要超過1位的規格化左移。同樣，如果d1則不需要全長的對階移位，但是需要一個壘長的規格化移位。在這種情況下，一位的對階和條件交換能夠通過階碼的低兩位預測，減少這一路徑的延時，因此，壘長的對階移位和全長的規格化移位是互斥的，並且，在關鍵路徑上只出現一個。這兩種情況可以表示為：當d1為CLOSE路徑；當d>1為FAR路徑。在每一個路徑的組成中．只有一個全長的移位。
（3）更進一步採用前導1的預測判定．在有效位加法完成之後，可能直接從運算元中預測結果前導0的數量。採用特殊的硬體前導1的預測可以與有效位加法並行處理。利用過三種情況，可以提高加法器的性能。按照數據分成兩個路徑實現有效位的運算：CLOSE路徑和FAR路徑。在這一最佳化中，為了增加加法器的性能的代價是一個附加的有效位加法器和一個多路進通器來選擇兩條路徑產生的最終結果。如果採用流水技術一個浮點加法器可分成四級流水，完成一個浮點加法運算需要4個周期。
Triple-data-path算法
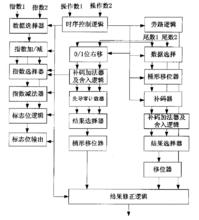
進一步的分析表明，當兩個運算元的指數差的絕對值比尾數的有效寬度還要大時，浮點加法的結果即為兩個運算元中較大的一個，加法運算不需要執行，因此根據Two-Path算法的原理，我們引入Triple-data-path算法。在此算法中，浮點加法過程分為三個通道，其中兩個數據通道為計算通道，另外一個為旁路數據通道。當指數差的絕對值大於尾數的位寬時，旁路通道為當前通道，否則計算通道為當前通道。Triple．data-path算法的結構圖如圖所示：
浮點加法器左數據通道尾數的移位只需單級的多路選擇器即可完成，由於有效數的預對準操作速度很快，所以加法完成後再進行先導0計數，而不採用先導零預測邏輯，這樣也能達到右數據通道相同的執行速度。由於先導零計數器遠比先導零預測邏輯簡單，所以簡化了硬體複雜度，降低了功耗。右數據通道有效數的預對準需要移多位，這一操作用桶形移位器來實現。由於減法是用補碼來實現的，所以補碼器只有在減法運算中才被激活。無論是左數據通道還是右數據通道，捨入的計算與尾數的加法運算並行執行，提高了加法的執行速度。結果選擇器根據捨入條件選擇合適的加法結果。時序控制邏輯用於為不同的輸入選擇合適的通道，並將它們傳送到所選的數據通道，同時產生不同的選通信號用於控制數據通道的狀態。標誌位邏輯用於標記異常情況，並進行相應的異常處理。
Triple-data-path浮點加法器結構在降低功耗方面有突出的優勢，但其流水線設計較複雜，硬體規模大，實現起來難度較大 。
