![數學模型[數學學科]](/img/c/0b8/nBnauM3XzADNxMTMxkzN0QjN1MTM5kjM5ADMxADMwAzMwIzL5czL1czLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg "數學模型[數學學科]")
簡介
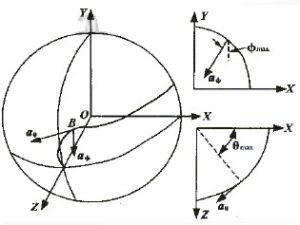s形刃球頭立銑刀的數學模型從廣義理解，數學模型包括數學中的各種概念，各種公式和各種理論。因為它們都是由現實世界的原型抽象出來的，從這意義上講，整個數學也可以說是一門關於數學模型的科學。從狹義理解，數學模型只指那些反映了特定問題或特定的具體事物系統的數學關係結構，這個意義上也可理解為聯繫一個系統中各變數間內的關係的數學表達。
數學模型所表達的內容可以是定量的，也可以是定性的，但必須以定量的方式體現出來。因此，數學模型法的操作方式偏向於定量形式。
分類
按模型的套用領域分類
生物數學模型
醫學數學模型
地質數學模型
數量經濟學模型
數學社會學模型
按是否考慮隨機因素分類
確定性模型隨機性模型
按是否考慮模型的變化分類
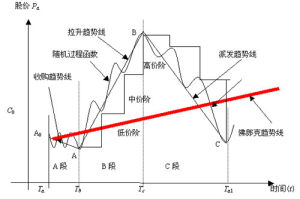“三段三階理論”框架和數學模型動態模型
按套用離散方法或連續方法分類
離散模型
連續模型
按建立模型的數學方法分類
幾何模型
微分方程模型
圖論模型
規劃論模型
馬氏鏈模型
按人們對事物發展過程的了解程度分類
白箱模型：指那些內部規律比較清楚的模型。如力學、熱學、電學以及相關的工程技術問題。
灰箱模型：指那些內部規律尚不十分清楚，在建立和改善模型方面都還不同程度地有許多工作要做的問題。如氣象學、生態學、經濟學等領域的模型。
黑箱模型：指一些其內部規律還很少為人們所知的現象。如生命科學、社會科學等方面的問題。但由於因素眾多、關係複雜，也可簡化為灰箱模型來研究。
基本原則
簡化原則
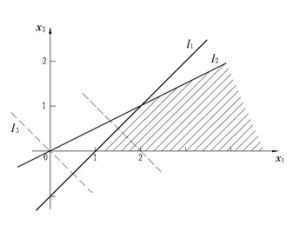線性規劃數學模型可推導原則
由數學模型的研究可以推導出一些確定的結果，如果建立的數學模型在數學上是不可推導的，得不到確定的可以套用於原型的結果，這個數學模型就是無意義的。
反映性原則
數學模型實際上是人對現實世界的一種反映形式，因此數學模型和現實世界的原型就應有一定的“相似性”，抓住與原型相似的數學表達式或數學理論就是建立數學模型的關鍵性技巧。
建立的要求
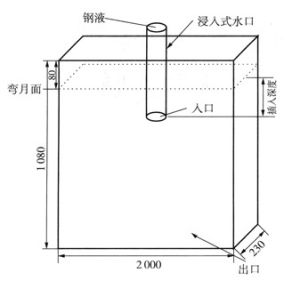數學模型的建立1）真實的、系統的、完整的反映客觀現象；
2）必須具有代表性；
3）具有外推性，即能得到原型客體的信息，在模型的研究實驗時，能得到關於原型客體的原因；
4）必須反映完成基本任務所達到的各種業績，而且要與實際情況相符合。
2、簡明實用。在建模過程中，要把本質的東西及其關係反映進去，把非本質的、對反映客觀真實程度影響不大的東西去掉，使模型在保證一定精確度的條件下，儘可能的簡單和可操作，數據易於採集。
3、適應變化。隨著有關條件的變化和人們認識的發展，通過相關變數及參數的調整，能很好的適應新情況。
構建的方法和步驟
模型準備
首先要了解問題的實際背景，明確建模目的，蒐集必需的各種信息，儘量弄清對象的特徵。
模型假設
根據對象的特徵和建模目的，對問題進行必要的、合理的簡化，用精確的語言作出假設，是建模至關重要的一步。如果對問題的所有因素一概考慮，無疑是一種有勇氣但方法欠佳的行為，所以高超的建模者能充分發揮想像力、洞察力和判斷力，善於辨別主次，而且為了使處理方法簡單，應儘量使問題線性化、均勻化。
模型構成
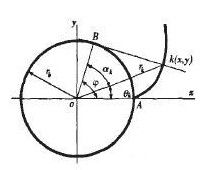漸開線齒廓曲線的數學模型模型求解
可以採用解方程、畫圖形、證明定理、邏輯運算、數值運算等各種傳統的和近代的數學方法，特別是計算機技術。一道實際問題的解決往往需要紛繁的計算，許多時候還得將系統運行情況用計算機模擬出來，因此編程和熟悉數學軟體包能力便舉足輕重。
模型分析
對模型解答進行數學上的分析。“橫看成嶺側成峰，遠近高低各不同”。能否對模型結果作出細緻精當的分析，決定了模型能否達到更高的檔次。還要記住，不論那種情況都需進行誤差分析，數據穩定性分析。
模型最佳化
對一個問題的假設和數學模型不斷加以修改，進行最最佳化處理。因為對一個問題或一類問題也可能有幾個模型，以對它們要進行比較，直到找到最優模型。
相關研究
花椰菜類幾何圖案數學模型出爐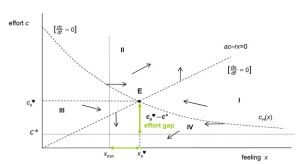
解釋離婚的情感動力學數學模型該成果有助於改良薄膜塗層技術，掌握它們在什麼情況下會表現出光滑、起皺或粗糙的形狀。這對計算機模擬生成材質紋理也非常有用。而且從概念上，這給他們提供了有關普適機制的線索，指導他們去描述一個整體中不同部分的結構是如何形成的，比如在有資源競爭的條件下，一個系統的不同部分之間會形成怎樣的結構。
科學家建立統計模型解答鳥類如何咿呀學語
埃默里大學生物學家塞繆爾-蘇伯與加利福尼亞大學的生理學家麥可-布雷納德通過研究鳴禽如何保持正確鳴叫，已經找到了一種統計學解釋，來解答為什麼對於大腦學習來說有的東西比其它的東西更加困難。
塞繆爾-蘇伯說道：“我們已經建造了第一個數學模型，使用鳥類先前具備的感覺運動經驗來預測它的學習能力。我們希望它能幫助我們理解其它物種以及人類的數學學習。”
他們的研究結果表明成年鳥類能夠更加快速和堅定的改正鳴叫中的小錯誤，這些發現被發表在《國家科學院院刊》上。
教學大綱
總學時：32學時適用專業：本科理工類、經濟類各專業
選用教材：姜啟源編《數學模型》（第二版）高教出版社出版
基本內容和要求
(一)數學建模的步驟、原理和方法：
1、了解數學建模的意義；
2、了解建立數學模型的基本知識、相關的基本概念；
3、掌握數學建模過程的幾個明顯的處理階段和流程；
4、通過實例了解數學模型的特點和學習方法；
5、了解全國大學生數學建模競賽。
(二)掌握數學建模思想方法：
1、數學建模概述
2、對現實問題的分析、提練、描述
3、幾種創造性思維方法
4、合理假設與信息處理
5、建立數學模型
6、數學軟體與模型求解
7、結果分析與靈敏度分析
8、模型的評價與推廣
9、論文摘要
(三)數學方法分類建模
1、初等數學方法建模；
2、線性規劃法建模；
3、非線性規劃法建模
4、微分方程建模；
5、層次分析法適用的建模問題和處理方法；
6、圖論方法建模；
7、機率分布方法建模。
(四)掌握一些特殊模型：
1、運輸問題模型；
2、經濟決策模型；
3、綜合評判模型；
4、捕魚業的持續收入；
5、幾種圖論模型；
6、效益的合理分配；
(五)數學建模論文的寫作：
1、知道數學建模競賽的規則及論文的評閱辦法；
2、掌握數學建模論文的幾個基本模組的數學方法。
說明
(一)本大綱根據我校的實際情況制定。
(二)課程類型：全校選修課。
(三)總則：本課程系統地介紹數學模型、數學建模和建模過程中的一些常用方法及數學建模實例，通過課堂教學和討論，使學生了解數學建模的特性及建模的基本方法，並初步具備對實際問題如何建模的能力以及培養良好的思考習慣和歸納分析能力，使學生在套用數學知識解決實際問題的能力有所提高。學習本課程的大部分內容只需要大學的微積分、線性代數、機率論等基本數學知識。
(四)教學目的及要求：逐步培養學生利用數學工具解決實際問題的能力。能夠將實際問題“翻譯”為數學語言，並予以求解，然後再解釋實際現象，甚至套用於實際。最終提高學生的數學素質和套用數學知識解決實際問題的能力。
(五)教學重點：對實際問題的分析；模型的合理假設；數學工具的恰當套用；模型的建立；模型的求解；模型結果的合理解釋；模型的套用；
(六)教學難點：對實際問題的分析；模型的合理假設；數學工具的恰當套用；模型結果的合理解釋與模型的套用；
(七)主要教學環節的組織：循序漸進的介入數學建模的思想，由簡入難的介紹各類數學模型；強化數學與計算機等其他工具的結合；對於一些重點教學環節，在突出對數學方法的同時，要重點講述數學方法與實際問題的一些必然的關聯性，使學生更具體的認識數學。對某些章節用到的不常用數學方法，予以簡單而有目的的介紹。
(八)大綱中教學基本要求從高到底分為理論部分：深入理解、一般理解、了解；運算部分：熟練掌握、一般掌握、知道。
