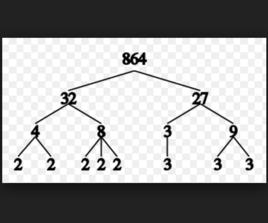
因子分解
完整的因子列表可以根據約數分解推導出,將冪從零不斷增加直到等於這個數。例如,因為45=3 ×5,45可以被3 ×5 ,3 ×5 ,3 ×5 ,3 ×5 ,3 ×5 ,和3 ×5 ,或者 1,5,3,9,15,和 45整除。相對應的,約數分解只包括約數因子。
實際套用
給出兩個大約數,很容易就能將它們兩個相乘。但是,給出它們的乘積,找出它們的因子就顯得不是那么容易了。這就是許多現代密碼系統的關鍵所在。如果能夠找到解決整數分解問題的快速方法,幾個重要的密碼系統將會被攻破,包括RSA公鑰算法和Blum Blum Shub隨機數發生器。
儘管快速分解是攻破這些系統的方法之一,仍然會有其它的不涉及到分解的其它方法。所以情形完全可能變成這樣:整數分解問題仍然是非常困難,這些密碼系統卻是能夠很快攻破。有的密碼系統則能提供更強的保證:如果這些密碼系統被快速破解(即能夠以多項式時間複雜度破解),則可以利用破解這些系統的算法來快速地(以多項式時間複雜度)分解整數。換句話說,破解這樣的密碼系統不會比整數分解更容易。這樣的密碼系統包括Rabin密碼系統(RSA的一個變體)以及Blum Blum Shub隨機數發生器。
當今的新進展
2005年,作為公共研究一部分的有663個二進制數位之長的RSA-200已經被一種一般用途的方法所分解。
如果一個大的,有 n個二進制數位長度的數是兩個差不多大小相等的約數的乘積,現在還沒有很好的算法來以多項式時間複雜度分解它。
這就意味著沒有已知算法可以在O( n)( k為常數)的時間內分解它。但是現在的算法也是比Θ(e)快的。換句話說,現在我們已知最好的算法比指數數量級時間要快,比多項式數量級時間要慢。已知最好的漸近線運行時間是普通數域篩選法(GNFS)。時間是:
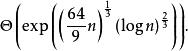 整數分解
整數分解對於平常的計算機,GNFS是我們已知最好的對付 n個二進制數位大約數的方法。不過,對於量子計算機,彼得·秀爾在1994年發現了一種可以用多項式時間來解決這個問題的算法。如果大的量子計算機建立起來,這將對密碼學有很重要的意義。這個算法在時間上只需要O( n),空間只要O( n)就可以了。 構造出這樣一個算法只需要2 n量子位。2001年,第一個7量子位的量子計算機第一個運行這個算法,它分解的數是15。
難度與複雜度
現在還不確切知道整數分解屬於哪個複雜度類。
我們知道這個問題的判定問題形式(“請問 N是否有一個比 M小的約數?”)是在NP與反NP之中。因為不管是答案為是或不是,我們都可以用一個素因數以及該素因數的素數證明來驗證這個答案。由秀爾算法可知,這個問題在BQP中。大部分的人則懷疑這個問題不在P、NP完全、以及反NP完全這三個複雜性類別中。如果這個問題可以被證明為NP完全或反NP完全,則我們便可推得NP=反NP。這將會是個很震憾的結果,也因此大多數人猜想整數分解這個問題不在上述的複雜性類別中。也有許多人嘗試去找出多項式時間的算法來解決這個問題,但是都尚未成功,因此這個問題也被多數人懷疑不在P中。
有趣的是,判定一個整數是否是素數則比分解該整數簡單許多。AKS算法證明前者可以在多項式時間中解決。 測試一個數是否為素數是RSA算法中非常重要的一環,因為它在一開始的時候需要找很大的素數。
整數分解算法
特殊用途算法
一個特別的因子分解算法的運行時間依賴它本身的未知因子:大小,類型等等。在不同的算法之間運行時間也是不同的。
•試除法
•車輪分解
•波拉德RHO算法
•代數群因式分解算法,其中包括Pollard'sp−1算法、Williams'p+1算法和Lenstra橢圓曲線分解法
•費馬素數判定法
•歐拉因式分解法
•特殊數域篩選法
一般用途算法
一般用途算法的運行時間僅僅依賴要分解的整數的長度。這種算法可以用來分解RSA數。大部分一般用途算法基於平方同餘方法。
•Dixon算法
•連分數分解法(CFRAC)
•二次篩選法
•理性篩選法
•普通數域篩選法
•Shanks' square forms factorization(SQUFOF)
其他算法
•秀爾算法