簡介
整數乘法法則是整數的運算法則之一，整數的乘法法則分三種情形表述：
1.一位數的乘法法則。兩個一位數相乘，可根據乘法定義用加法計算，通常可利用乘法表直接得出任意兩個一位數的積。
2.多位數的乘法法則。依次用乘數的各個數位上的數，分別去乘被乘數的每一數位上的數，然後將乘得的積加起來。
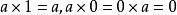整數乘法法則3.對於任意數a，有。
乘法表
乘法表在我國很早就已產生。
遠在春秋戰國時代，九九歌就已經廣泛地被人們利用著。在當時的許多著作中，已經引用部分乘法口訣。最初的九九歌是以“九九八十一”起到“二二如四”止，共36句口訣。
發掘出的漢朝“竹木簡”以及敦煌發現的古“九九術殘木簡”上都是從“九九八十一”開始的。“九九”之名就是取口訣開頭的兩個字。
大約公元5～10世紀間，“九九”口訣擴充到“一一如一”。
大約在宋朝（公元11、12世紀），九九歌的順序才變成和現代用的一樣，即從“一一如一”起到“九九八十一”止。元朱世傑著《算學啟蒙》一書所載的45句口訣，已是從“一一”到”九九“，並稱為九數法。現在用的乘法口訣有兩種，一種是45句的，通常稱為小九九；還有一種是81句的，通常稱為大九九。書中記載，大九九最早見於清陳杰著的《算法大成》。
計算方法
使用鉛筆和紙張乘數的常用方法需要一個小數字（通常為0到9的任意兩個數字）的存儲或查詢產品的乘法表，但是一種農民乘法算法的方法不是。
將數字乘以多於幾位小數位是繁瑣而且容易出錯的。發明了通用對數以簡化這種計算。幻燈片規則允許數字快速乘以大約三個準確度的地方。從二十世紀初開始，機械計算器，如Marchant，自動倍增多達10位數。現代電子計算機和計算器大大減少了用手倍增的需要。
歷史算法
在埃及，希臘，印度和中華文明中記載了繁殖方法。
公元前約公元前十八萬公元至二千零二十年的三叉骨，暗示了中非舊石器時代上升的知識。
埃及人
在阿姆斯紙莎草紙中記載的埃及整數和分數乘法的方法是連續添加和加倍。例如，要找到13和21的乘積，必須雙倍21次，得到2×21 = 42，4×21 = 2×42 = 84,8×21 = 2×84 = 168.完整的產品可以然後通過添加在雙倍序列中找到的適當術語來找到：13×21 =（1 + 4 + 8）×21 =（1×21）+（4×21）+（8×21）= 21 + 84 + 168 = 273。
巴比倫人
巴比倫人使用了一個十六進制位置數字系統，類似於現代十進制。因此，巴比倫的乘法非常類似於現代十進制乘法。由於記憶60×60不同產品的相對困難，巴比倫數學家使用乘法表。這些表由某個主體號n：n，2n，...，20n的前20個倍數列表組成。其次是10n：30n 40n和50n的倍數。然後計算任何六進制產品，例如53n，只需要從表中計算出50n和3n。
中國人
在公元前300年前的數學文本《周髀算經》和《算術九章》中，乘法計算用字寫出，雖然早期的中國數學家使用了涉及加法，減法，乘法和除法的羅德微積分。 Al Khwarizmi在9世紀初向阿拉伯國家介紹了這些地名十進制算術算法。
