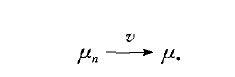
概念
機率測度的一種收斂性。若{μ，n≥1}是(R，B)上的機率測度序列(其中R為n維實空間，B為n維波萊爾域)，若存在(R，B)上的測度μ(滿足μ(R)≤1)，使得對一切μ的連續區間(a，b](即滿足μ([a，b]\(a，b))=0)，均有μ((a，b])→μ((a，b])，其中：
(a，b]={(x，x，…，x)：a<x≤b，i=1，2，…，n}，
[a，b]={(x，x，…，x)：a≤x≤b，i=1，2，…，n}
為R中有限區間，則稱機率測度序列{μ}淡收斂到μ。記為：
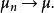淡收斂由奧地利數學家黑利(Helly，E.)選擇定理的推廣知，(R，B)上任一機率測度序列都有淡收斂的子序列。如果{μ，n≥1}的一切淡收斂的子序列均淡收斂到同一極限μ，則{μ}淡收斂到μ。若μ本身是機率測度，則稱{μ}弱收斂到μ。記為：
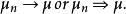淡收斂淡收斂和弱收斂的概念可以推廣到一般的距離可測空間或拓撲可測空間上。
弱收斂
點列的弱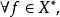收斂
淡收斂定義1設X為賦范線性空間，x，x∈X，若對有
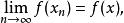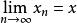淡收斂
淡收斂則稱{x} 弱收斂於x，記作w-.
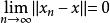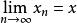淡收斂 淡收斂註：設X為賦范線性空間，x，x∈X，當時，稱{x} 強收斂於x，記作s-.
性質
1.由點列強收斂可推出其弱收斂。
證明：由
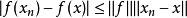淡收斂可證。並且強極限存在時必等於其弱極限，反之卻不然。
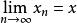淡收斂2.設X為賦范線性空間，x，x∈X，則w-，若且唯若
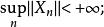淡收斂（1）
（2）存在X*上一個稠密集Y，使得
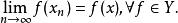淡收斂3.設X為一致凸的賦范線性空間，則X中的點列{x}強收斂於x的充要條件是{x}弱收斂於x，且有
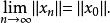淡收斂泛函列的弱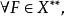收斂
淡收斂定義3設X為賦范線性空間，X*為其對偶空間，f，f ∈X*，若對有
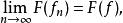淡收斂則稱{f} 弱 收斂於T.
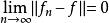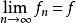淡收斂
淡收斂註：1.設X為賦范線性空間，X*為其對偶空間，f，f ∈X*，當時，稱{f} 強收斂於f，記作s-；
淡收斂2.設X為賦范線性空間，X*為其對偶空間，f，f ∈X*，若對有
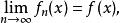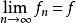淡收斂 淡收斂則稱{f} 弱* 收斂於f，記作w*-.
性質
當X為自反空間時，{f}弱收斂與{f}弱*收斂等價。
設X為Banach空間，f，f ∈X*，則{f}弱*收斂於f，若且唯若
1.當X為自反空間時，{f}弱收斂與{f}弱*收斂等價。
2.設X為Banach空間，f，f ∈X*，則{f}弱*收斂於f，若且唯若
（1）
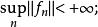淡收斂（2）存在X上的稠密集X，使得
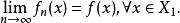淡收斂機率測度
機率測度是機率論、遍歷理論等數學分支中常用的一種重要的有限測度。設(Ω，F)是可測空間，μ是F上的測度.若μ(Ω)=1，則稱μ為機率測度，並稱(Ω，F，μ)為機率空間。20世紀完成的勒貝格測度和勒貝格積分理論以及隨後發展起來的抽象測度和積分理論，為機率論公理體系的確立奠定了理論基礎。機率測度和機率空間就是在這樣的歷史背景下產生的一種重要測度和測度空間。
測度
數學上， 測度（Measure）是一個函式，它對一個給定集合的某些子集指定一個數，這個數可以比作大小、體積、機率等等。傳統的積分是在區間上進行的，後來人們希望把積分推廣到任意的集合上，就發展出測度的概念，它在數學分析和機率論有重要的地位。
測度論是實分析的一個分支，研究對象有σ代數、測度、可測函式和積分，其重要性在機率論和統計學中都有所體現。
定義1：構造一個集函式，它能賦予實數集簇М中的每一個集合E一個非負擴充實數mE。我們將此集函式稱為E的測度。
定義2：設Γ是集合X上一σ代數，ρ ：Γ → R∪{ +∽ }是一集合函式，且ρ滿足：
（1）（非負性）對任意的A∈Γ，有ρ(A)≧0;
（2）（規範性）ρ(Φ) = 0；
（3）（完全可加性） 對任意的一列兩兩不交集合A，A，……，A，……有ρ(∪n A)=∑n ρ（A）
則稱ρ是定義在X上的一個測度，Γ中的集合是可測集，不在Γ中的集合是不可測集。特別的，若ρ(X) = 1 ，則稱ρ為機率測度。
