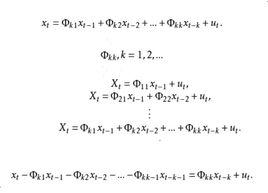偏自相關函式的定義
用Φx+Φx+...+Φx+u，表示k階自回歸式中第j個回歸係數，則k階自回歸模型表示為
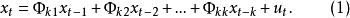偏自相關函式
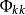偏自相關函式其中是最後一個係數。若把看作滯後期k的函式，則稱
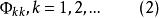偏自相關函式
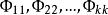偏自相關函式為 偏自相關函式。它由下式中的組成。
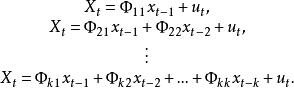偏自相關函式 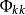偏自相關函式
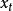偏自相關函式
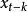偏自相關函式
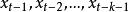偏自相關函式因自相關函式中每一個回歸係數恰好表示與在排除了其中間變數影響後的自相關係數，即
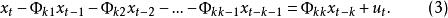偏自相關函式 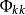偏自相關函式中的，所以偏自相關函式由此得名 。
偏自相關函式求解
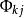偏自相關函式
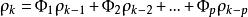偏自相關函式用表達Yule-Walker方程，得，得
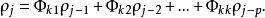偏自相關函式用矩降形式表示上式：
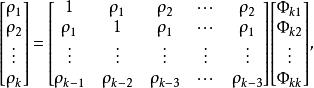偏自相關函式
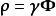偏自相關函式或為：
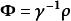偏自相關函式則:.
將k=1,2,...代人上式連續求解、可求得偏自相關函式
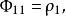偏自相關函式
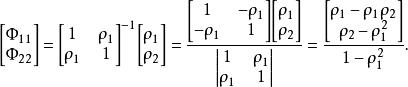偏自相關函式
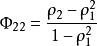偏自相關函式其中。
自回歸模型的偏自相關函式
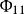偏自相關函式 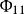偏自相關函式 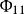偏自相關函式對於AR(1)過程，當k=1時，≠0；當k>1時，=0，所以AR(1)過程的偏自相關函式特徵是在k=1時出現峰值(=ρ)，然後截尾，如圖1所示。
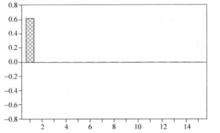圖1(a)AR(1)過程的偏自相關函式圖(φ₁₁>0)
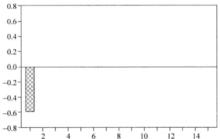圖1(b)AR(1)過程的偏自相關函式圖(φ11<0) 偏自相關函式 偏自相關函式對於AR(2)過程，當k<2時，≠0；當k>2時，=0。偏自相關函式在滯後期2以後有截尾特性。
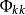偏自相關函式 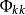偏自相關函式對於AR(p)過程，當k≤p時，≠0；當k>p時；=0。偏自相關函式在滯後期p以後有截尾特徵，因此可用此特徵識別AR(p)過程的階數 。
移動平均模型的偏自相關函式
MA(1)過程的偏自相關函式呈指數衰減特徵。若θ>0，偏自相關函式呈交替改變符號式指數衰減；若θ<0，偏自相關函式呈負數的指數衰減，如2所示。
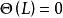偏自相關函式 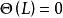偏自相關函式對於MA(2)過程，若的根是實數，偏自相關函式由兩個指數衰減形式疊加而成。若的根是虛數，偏自相關函式呈正弦衰減特徵(拖尾特徵)。
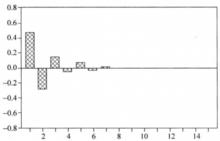圖2(a) MA(1)過程的偏自相關函式圖θ₁>0
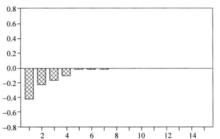圖2(b) MA(1)過程的偏自相關函式圖θ₁<0因為任何一個可逆的MA(q)過程都可以轉換成一個無限階的、係數按幾何遞減的AR過程，所以MA(q)過程的偏自相關函式呈緩慢衰減特徵，稱拖尾特徵 。
ARMA(p,q)過程的偏自相關函式
偏自相關函式ARMA(p,q)過程的偏自相關函式也是無限延長的，其表現形式與MA(q)過程的偏自相關函式相類似。根據模型中移動平均分量的階數q以及參數(i= 1,2,...,q)的不同，偏自相關函式呈指數衰減和(或)正弦衰減混合形式。
對於時間序列數據，偏自相關函式通常是未知的。估計的偏自相關函式
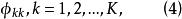偏自相關函式
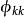偏自相關函式 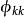偏自相關函式稱為偏相關圖。其中是對式(1)中的估計。偏相關圖是由k個估計的偏自相關係數組成的係數列。對於分析非季節序列的偏相關圖，實際中取k=15就足可以了。
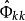偏自相關函式的方差近似為T。當T充分大時，近似有
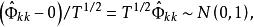偏自相關函式 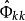偏自相關函式
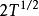偏自相關函式所以在觀察偏相關圖時，若的絕對值超過(2個標準差)，就被認為顯著不為零。
因為AR過程和ARMA過程中AR分量的偏自相關函式具有截尾特徵，所以可利用偏相關圖估計自回歸過程的階數p。偏相關圖是識別AR過程和ARMA過程中AR分量階數的一個重要方法 。
