定義
定義一
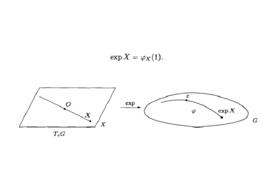
由李群的李代數到李群的一種解析映射.若G為李群,e為單位元素,T(G)為G中點e的切空間,任取X∈T(G),則惟一存在左不變向量場X,使得X=dL(X),∀g∈G.任給左不變向量場X,構作運算元
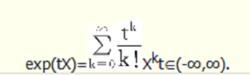 指數映射
指數映射任意取定單位坐標鄰域U,點x=(x,x,…,x),記
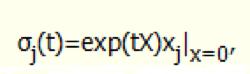 指數映射
指數映射當|t|<ε,(σ,σ,…,σ)為U中點.於是,在U中有一條單參數解析曲線
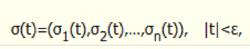 指數映射
指數映射記exp(tX)=σ(t),|t|<ε.它可開拓到t∈(-∞,∞),使得
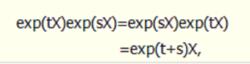 指數映射
指數映射且exp(tX),t∈(-∞,∞)為G之一維連通李子群.反之,任意一維連通李子群惟一決定左不變向量場X,使得此李子群為exp(tX).於是,有映射exp:J→G,稱為指數映射,這裡J為李群G的李代數.指數映射是建立李群和它的李代數間的關係的重要工具,在李群理論中占有重要的地位.
且exp(tX),∀t∈(-∞,∞)為G之一維連通李子群.反之,任意一維連通李子群惟一決定左不變向量場X,使得此李子群為exp (tX ).於是,有映射exp:J→G,稱為指數映射,這裡J為李群G的李代數.指數映射是建立李群和它的李代數間的關係的重要工具,在李群理論中占有重要的地位 .
定義二
切平面到曲面的一種映射.設T是曲面S在P點的切平面,指數映射是從切平面T到曲面S上的一個對應關係,記成exp:T→S,定義如下:設v是曲面S在P點的一個切向量,過P作S上切於v的測地線,在此測地線上取一點M使得從P到M的弧長正好等於v的長度|v|,則定義expv=M .
引理1 對於曲面M上的每點p0,存在包含p0的一個坐標鄰域U及常數ε>0,使得對於每點p∈U和p點切空間T(M)中每個長度小於ε的切向量v,都有唯一的一條滿足初始條件
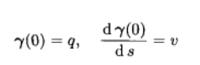 指數映射
指數映射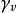 指數映射
指數映射的測地線::(-2,2)→M
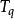 指數映射
指數映射設q∈M,v∈(M),若存在測地線
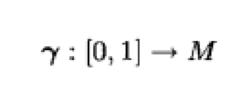 指數映射
指數映射滿足初始條件
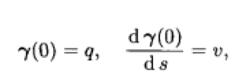 指數映射
指數映射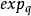 指數映射
指數映射那么點γ(1)∈M叫做在q點切向量v的指數映像,用(v)表示γ(1),而映射
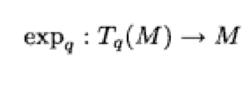 指數映射
指數映射稱為在q點的指數映射.於是,滿足初始條件的唯一測地線可表達為
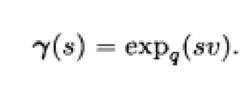 指數映射
指數映射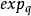 指數映射
指數映射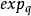 指數映射
指數映射根據引理1 當||v|| 充分小時,(v)是確定的.一般地說,對於長度較長的向量v,指數映像(v)未必能確定.然而如果能確定,則總是唯一的.
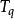 指數映射
指數映射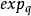 指數映射
指數映射定義 若對於任何點q∈M和任何向量v∈(M),指數映像(v)總是確定的,則曲面M稱為測地完備的.
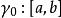 指數映射
指數映射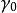 指數映射
指數映射顯然,測地完備性等價於下述要求:對於每段測地線段→M,總能夠把延拓成無限長的測地線:
γ:R→M
因此,我們也可把後者作為測地完備性的定義 .
與李代數
研究李代數元素的另一種方法是把它看作群上的左不變向量場.迄今為止,我們只是討論單位元處的向量,對於向量場,需要涉及所有群元素的切線.將一個群元素在左側相乘。就定義了群流形的一個同構g:G→G,其中g(g₁):gg₁,群在它的基礎流形上的這個作用誘導出在該流形向量場上的作用.左不變向量場關於這個作用是固定不變的.將任何左不變向量場限制到單位元上的切向量。即一個李代數元素.而給出一個單位元上的切向量。就能產生一個左不變向量場.我們需要做的就是左平移原始向量到流形上的每個點.如果X是一個矩陣。描述單位元處的切向量。則在群的點g處的切向量定義為gX.因此,單位元的切向量和左不變向量場之間是一一對應的.
這些左不變向量場的積分曲線在後面起重要的作用.向量場的積分曲線是在每一點都與該場相切的曲線.對於左不變向量場。這個曲線滿足如下微分方程: .
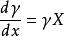 指數映射
指數映射這個方程有解析解,通過單位元素的解是
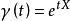 指數映射
指數映射矩陣X的指數可以展開成冪級數:
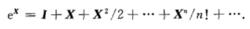 指數映射
指數映射對於矩陣指數有如下關係:
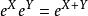 指數映射
指數映射若且唯若[X,Y]=0.
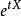 指數映射
指數映射這表示只有當指數是可交換時,指數積運算時指數才可以相加.當然,元素t1X和t2X是可交換的,這表示形如的群元素構成子群:
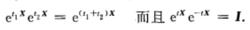 指數映射
指數映射它們是群的一維或單參數子群.用這種方法。每個李代數元素都產生一個單參數子群.
指數函式也可以被看作給出了從李代數到群的映射。這個映射通常既不是單射也不是滿射,但是在單位元附近它是同胚映射.即在李代數上存在0的鄰域同胚映射到群的單位元的鄰域.在這個鄰域存在一個逆映射。通常被稱作對數,由眾所周知的Mercator級數定義。即
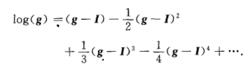 指數映射
指數映射當g遠離單位元時,級數不收斂.
矩陣指數的行列式是矩陣跡的指數:
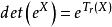 指數映射
指數映射矩陣的跡Tr()是它的對角線元素之和.如果矩陣X的特徵值都不相同。那么這個關係能夠通過對角化矩陣簡單地證明.即使在一般情況下,這個關係也是正確的.由這個關係可以得到:矩陣指數的行列式為1若且唯若矩陣是跡為0的.這就是李代數so(n),su(n)和sl(n)由跡為0的矩陣構成的原因.
對於某些李代數,我們能夠更詳細地確定它的指數映射.例如。考慮su(2),典型的李代數元素m用伴隨表示可以描述成如下形式的矩陣:
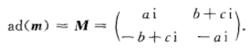 指數映射
指數映射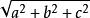 指數映射
指數映射通過簡單的計算可以得到 M²=(a²+b²+c²) I₂.如果要求 M= X。則得到 X²=- I₂.由此將det( M)=a²+b²+c²看作是參數t²。將它們代入到指數定義得到
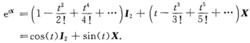 指數映射
指數映射這也可以用原始的李代數元素 M寫作
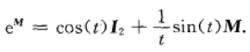 指數映射
指數映射可以由M的行列式得到t.
上述關係是線性的。這意味著對數也能夠簡單地求出.如果U是su(2)的元素。則
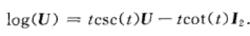 指數映射
指數映射這裡,t可以根據等式Tr( U)=2cos(t)得到.如上所述,這個對數並不是在整個群上有定義,顯然上面得到的公式在t=±π弧度時無意義 .