二維拋物線坐標系
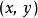拋物線坐標系
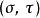拋物線坐標系直角坐標 可以用二維拋物線坐標表示為
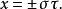拋物線坐標系
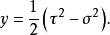拋物線坐標系
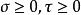拋物線坐標系其中，。
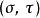拋物線坐標系 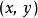拋物線坐標系反算回來，二維拋物線坐標可以用直角坐標 表示為
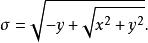拋物線坐標系
拋物線坐標系
拋物線坐標系坐標為常數的曲線形成共焦的，凹性向上的（往 +y-軸）拋物線：
拋物線坐標系
拋物線坐標系而坐標為常數的曲線形成共焦的，凹性向下的（往 -y-軸）拋物線：
拋物線坐標系這些拋物線的焦點的位置都在原點。
二維標度因子
拋物線坐標系拋物線坐標的標度因子相等：
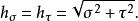拋物線坐標系因此，面積的無窮小元素是
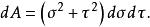拋物線坐標系拉普拉斯運算元是
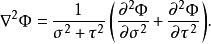拋物線坐標系
拋物線坐標系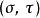 拋物線坐標系其它微分運算元，像都可以用 坐標表示，只要將標度因子代入在正交坐標系條目內的一般公式。
三維拋物線坐標系
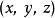拋物線坐標系
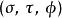拋物線坐標系將二維的拋物線坐標系繞著拋物線的對稱軸旋轉，則可以得到三維的拋物線坐標系，又稱為 旋轉拋物線坐標系。將對稱軸與 z-軸排列成同直線；而拋物線坐標系的共焦點與直角坐標系的原點同地點。直角坐標可以用三維拋物線坐標表示為
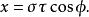拋物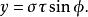線坐標系
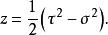拋物線坐標系
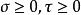拋物線坐標系 拋物線坐標系
拋物線坐標系其中， ，方位角 定義為
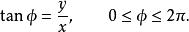拋物線坐標系 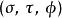拋物線坐標系 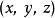拋物線坐標系反算回來，三維拋物線坐標可以用直角坐標表示為
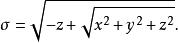拋物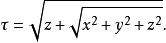線坐標系
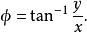拋物線坐標系
拋物線坐標系 拋物線坐標系每一個-坐標曲面都是共焦的，凹性向上的（往 +z-軸） 拋物曲面：
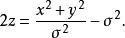拋物線坐標系 拋物線坐標系而每一個>-坐標曲面都是共焦的，凹性向下的（往 -z-軸） 拋物曲面：
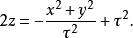拋物線坐標系這些拋物曲面的焦點的位置都在原點。
三維標度因子
三維標度因子為：
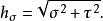拋物線坐標系
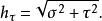拋物線坐標系
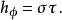拋物線坐標系
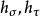拋物線坐標系我們可以觀察出，標度因子與二維標度因子相同。因此，體積的無窮小元素是
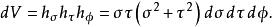拋物線坐標系拉普拉斯運算元是
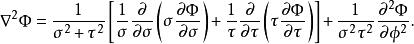拋物線坐標系 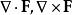拋物線坐標系 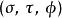拋物線坐標系其它微分運算元，像，都可以用坐標表示，只要將標度因子代入在正交坐標系條目內的一般公式。
