正文
在物理學史上,人們對落體運動的認識,經歷過較長期的爭論。16世紀以前的學者對各種物體下落的快慢有不同的觀點。希臘哲學家亞里士多德曾錯誤地認為,物體越重下落越快,而且認為不考慮空氣阻力時也是這樣。伽利略在1604年否定了上述觀點,指出物體下落的高度與時間的平方成正比,而與重量無關,即落體運動是勻加速的;通常看到不同物體下落之所以有快慢,並不是由於重量不同,而是由於空氣阻力。伽利略用實驗證實了他的理論。他所引進的加速度概念和他所發現的勻加速運動規律促進了動力學的重大發展。介質阻力 介質的阻力決定於介質的物理性質、物體運動的速度和物體的形狀和尺寸。如果物體的尺寸很小,速度也很小(例如小於每秒24米),則可設阻力與速度成正比;這個定律對極緩慢的運動是足夠準確的。但在物體尺寸和運動速度的很大範圍內,可認為阻力與速度的平方成正比;現代流體力學的理論和實驗都證明了這個定律。如果運動的速度接近聲速,則阻力的增大比速度的平方還快。如果速度再增加,阻力變化的規律就更為複雜。與阻力有關的數據須通過實驗及理論研究得到。
①阻力與速度成正比 設小物體Q(見圖) 在靜止液體中從靜止開始下沉,液體阻力的大小與物體的速度成正比,比例係數為μ。μ 的數值與液體的性質、物體的形狀有關。設阻力R=-μ,則物體的運動微分方程為:
,
式中g為重力加速度;為R在鉛垂軸x上的投影。積分一次,代入初始條件:t=0,v0=0,得到物體Q下沉速度的表示式: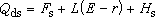 。
。
。
②阻力與速度的平方成正比 設阻力R=μv2,且用記號=v,,則物體Q的運動微分方程為:。
積分上式,代入初始條件:t=0時,v0=0,並設,得速度表示式: 。
。
。
極限速度 物體在地球重力和介質阻力作用下鉛直降落的最大速度。自由落體的加速度為g=9.80米/秒2,其速度與時間t成正比,直到與地面相碰為止。然而在有阻力的介質中運動時,例如降落傘和炸彈從飛機上降落時,空氣阻力限制它們速度的增長。介質對物體的阻力可寫作:R=μf(v),
式中μ 同介質的密度和物體在運動方向上的投影面積成正比;f(v)為落體速度的函式,當v=0,f(v)=0。物體在重力和介質阻力作用下,鉛直降落時的運動微分方程為:。
從上式看到,如運動開始時速度為零(阻力等於零),則物體的加速度等於g;此後有了速度即出現阻力,因而加速度減小。但由於速度的增長,阻力也在增長,因而物體的加速度愈來愈小,即速度的增長愈來愈慢。當速度增加到使阻力等於重力,即mg-μf(v)=0時,
物體的加速度等於零。此時,速度達到極限值。從上式解出的速度v*就稱為極限速度。此後落體即以極限速度v*勻速降落。如果R=μv,得到極限速度
v*=mg/μ。
如果R=μv2,例如降落傘降落時所受的阻力,得到極限速度 。
。
自由落體運動 阻力可以忽略的落體運動。這種情況下,落體只在重力作用下運動,其加速度為g。g的數值由實驗求出,一般取為9.80米/秒2。
自由落體的運動微分方程為m=mg。通過積分並代入初始條件:t=0,x0=0,v0=0,可得到自由落體運動的三個公式: 式中v和h分別為任一時刻物體的下落速度和下降高度。