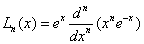定義
在數學中，拉蓋爾多項式定義為拉蓋爾方程的標準解。下列為拉蓋爾方程：
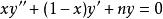拉蓋爾多項式
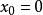拉蓋爾多項式 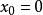拉蓋爾多項式此方程只有當n為非負時才有非平凡解。 是拉蓋爾方程的正則奇點。在 及其鄰域上為有限的級數解是
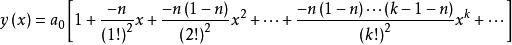拉蓋爾多項式級數的收斂半徑為無限大。
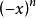拉蓋爾多項式
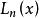拉蓋爾多項式如n為整數，解y（x）退化為n次多項式。用適當的常數乘這些多項式，使最高次冪項成為 就叫作拉蓋爾多項式，記作 ，
拉蓋爾多項式由羅德里格公式推導出公式 ，如下：
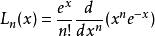拉蓋爾多項式它可以用遞推關係表達，如下：
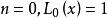拉蓋爾多項式
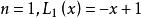拉蓋爾多項式
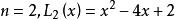拉蓋爾多項式拉蓋爾多項式的遞推關係也可以表現為 ：
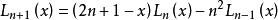拉蓋爾多項式
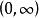拉蓋爾多項式此多項式是區間 上函式全體按照如下定義內積時的標準正交多項式：
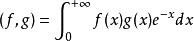拉蓋爾多項式廣義
定義
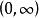拉蓋爾多項式
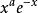拉蓋爾多項式
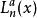拉蓋爾多項式稱在 上伴隨核函式 的標準正交多項式為廣義拉蓋爾多項式，記為 。廣義拉蓋爾多項式也可以由如下的羅德里格公式給出：
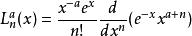拉蓋爾多項式
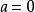拉蓋爾多項式當 時，廣義拉蓋爾多項式退化為標準拉蓋爾多項式。
廣義拉蓋爾多項式有如下解析表達式：
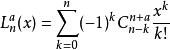拉蓋爾多項式廣義拉蓋爾多項式有如下遞推關係 ：
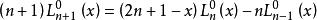拉蓋爾多項式
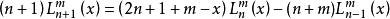拉蓋爾多項式性質
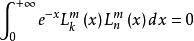拉蓋爾多項式正交性：
平方積分：
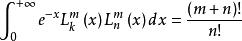拉蓋爾多項式相關恆等式
關於一般拉蓋爾多項式和拉蓋爾多項式，可以得到以下兩個恆等式 ：
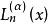拉蓋爾多項式
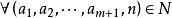拉蓋爾多項式
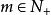拉蓋爾多項式
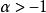拉蓋爾多項式定理1：設 是一般拉蓋爾多項式，那么， 及 ,當 時，有恆等式
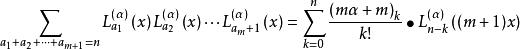拉蓋爾多項式
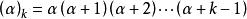拉蓋爾多項式其中， 。
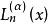拉蓋爾多項式 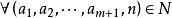拉蓋爾多項式 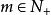拉蓋爾多項式定理2：設 是拉蓋爾多項式，那么， 及 ，有恆等式
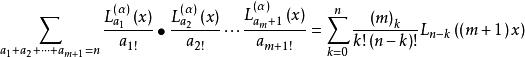拉蓋爾多項式