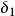正文
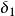應變能以一維問題為例，一個截面積為A、長度為L的等截面直桿在軸向外力P1的作用下伸長 （圖1）。如果不考慮變形過程中的動力效應和溫度效應，則外力作的功W全部貯存到桿中，變成了桿的應變能U，其值為：
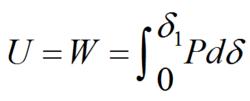應變能
應變能
應變能 應變能式中P為變形過程中與伸長量 對應的載荷。在圖2所示的P－ 曲線中，曲線下方的面積相當於桿中的應變能。而和曲線上方的面積相應的為余應變能（簡稱余能），記為U*，其值為：
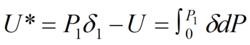應變能
應變能
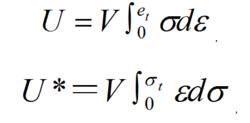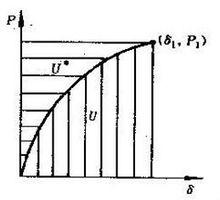應變能
應變能
應變能 應變能 應變能 應變能 應變能式中 V =LA為桿的體積； =P/A為桿中的應力； = /L為桿中的應變； 1、 1分別為P1、 1對應的應力和應變。如果桿的材料為線彈性的（即應力和應變成正比），則應變能和余能相等，即
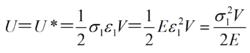應變能式中E為彈性模量。
在三維問題中，有六個獨立的應力分量和六個獨立的應變分量。在小變形的情況下，每個應力分量在相應的應變分量上作功，因此應變能和余能的表達式都包括六項：
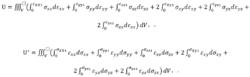應變能 應變能 應變能 應變能 應變能 應變能 應變能 應變能 應變能 應變能 應變能 應變能 應變能式中xx、yy、zz、xy、xz、yz為物體在載入過程中的應力分量；xx、yy、zz、xy、xz、yz分別為與上述應力分量相應的應變分量；積分上限的下標1表示載入終點。對於線彈性體則有：
應變能