概念
單位體積的彈性應變能稱為彈性應變能密度。
彈性應變能
彈性體受外力作用後,不可避免地要產生變形,同時外力的勢能也要產生變化。根據熱力學的觀點,外力所做的功,一部分將轉化為彈性體的動能,一部分將轉化為內能;同時,在物體變形過程中,它的溫度也將發生變化,或者從外界吸收熱量,或者向外界發散熱量。現分析彈性體內任一有限部分∑的外力功和內能的變化關係,設彈性體內取出部分Σ的閉合表面為 S,它所包圍的體積為 V。以 δ W表示外力由於微小位移增量在取出部分Σ上所作的功, δ U表示在該微小變形過程中取出部分Σ的內能增量, δ K表示動能增量, δ Q表示熱量的變化(表示為功的單位),根據熱力學第一定律,則有
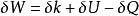 應變能密度
應變能密度我們首先假設彈性體的變形過程是絕熱的,也就是假設在變形過程中系統沒有熱量的得失。再假設彈性體在外力作用下的變形過程是一個緩慢的過程,在這個過程中,荷載施加得足夠慢,彈性體隨時處於平衡狀態,而且動能變化可以忽略不計(這樣的載入過程稱為準靜態載入過程),則根據上式表示的熱力學第一定律,外力在變形過程中所做的功將全部轉化為內能儲存在彈性體內部。這種貯存在彈性體內部的能量是因變形而獲得的,故稱之為彈性變形能或彈性應變能。由於彈性變形是一個沒有能量耗散的可逆過程,所以,卸載後,彈性應變能將全部釋放出來。下面,推導單位體積彈性應變能的表達式。
仍以 X、Y、Z表示單位體積的外力,表示作用在彈性體內取出部分Σ表面上單位面積的內力。對上述的準靜態載入過程,可以認為彈性體在外力作用下始終處於平衡狀態。外力所作的功W包含兩個部分:一部分是體力 X、Y、Z所作的功 W1,另一部分是面力所作的功W,它們分別為
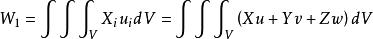 應變能密度
應變能密度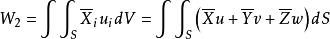 應變能密度
應變能密度故
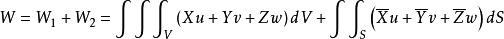 應變能密度
應變能密度因此,外力由於微小位移增量在取出部分Σ上所作的功 δW 可以表示為
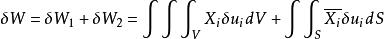 應變能密度
應變能密度將平衡微分方程和靜力邊界條件代入上式,並利用散度定理,上式可化為
 應變能密度
應變能密度最終可推得相應的內能增量δU為
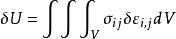 應變能密度
應變能密度定義函式u(ε ),使之滿足
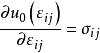 應變能密度
應變能密度該定義式稱為格林(Green)公式。
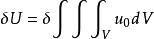 應變能密度
應變能密度則有。
由上式可以看出,函式u(ε )表示單位體積的彈性應變能,故稱之為彈性應變能密度函式(或彈性應變比能函式),簡稱為應變能。由於彈性應變能密度函式表示彈性體的內能概念,因此,它必然是一個勢函式,故也稱之為彈性勢函式。
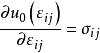 應變能密度
應變能密度對取積分可得
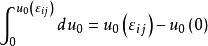 應變能密度
應變能密度這裡,u(ε )和u(0)分別表示物體變形之後和未變形時的彈性應變能密度。通常,取u0(0)=0,於是有
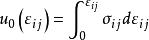 應變能密度
應變能密度根據格林公式,假如u(ε )的具體函式形式能夠確定的話,那么,彈性體的應力與應變之間的關係也就完全確定了。這表明,彈性應變能密度函式是彈性材料本構關係的另一種表達形式。
軸向拉壓桿
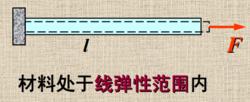 應變能密度
應變能密度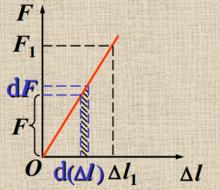 應變能密度
應變能密度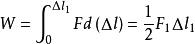 應變能密度
應變能密度 應變能密度
應變能密度應變能:。
應變能密度:桿件應變能與桿件體積之比。
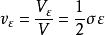 應變能密度
應變能密度應變能 —— 是桿件參數,與桿件變形有關。
應變能密度 —— 與桿件無關,只與應力狀態有關。
三向應力狀態
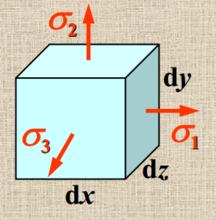 應變能密度
應變能密度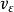 應變能密度
應變能密度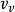 應變能密度
應變能密度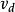 應變能密度
應變能密度應變能密度=體積改變能密度+形狀改變能密度。
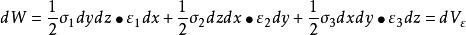 應變能密度
應變能密度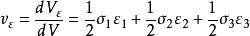 應變能密度
應變能密度體積改變能密度:
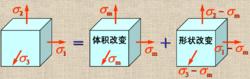 應變能密度
應變能密度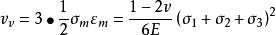 應變能密度
應變能密度形狀改變能密度:
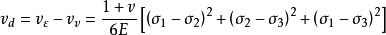 應變能密度
應變能密度