簡介
在流體力學中, Kc數( Keulegan–Carpenter number)是一個無量綱數,用來描述一個在振盪流場中的物體,所受到的粘性力相對慣性力之間的關係,也可可以用在一物體在靜止流體中振盪的情形。Kc數小表示慣性力的影響比粘性力要大,Kc數大表示(紊流)粘性力的影響較大。
Kc數的定義如下
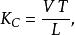 Kc數
Kc數其中 V為流速振盪的振幅(若是物體振盪的情形,則為物體速度的振幅); T為振盪的周期; L為物體的特徵長度,若物體為一圓柱,其特徵長度為其直徑。
在探討海浪對沉積物運移的影響時,會使用另一個相關的位移參數δ(displacement parameter)來表示:
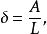 Kc數
Kc數其中 A為在振盪流場中流體粒子的偏移幅度,若流場以弦波運動, A可以用 V和 T表示 A=VT/(2π),則
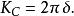 Kc數
Kc數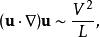 Kc數
Kc數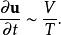 Kc數
Kc數若將納維-斯托克斯方程的加速度項進行尺度分析,也可以找到Kc數:對流加速度:局部加速度:將以上二式相除即可得到Kc數。
斯特勞哈爾數和Kc數有些相近。斯特勞哈爾數在形式上是Kc數的倒數。斯特勞哈爾數可以求得將一物體置入穩定的流場後,其產生旋渦分離的頻率,可以作為流場不穩定性的指標。而Kc數是和不穩定流場對物體的影響有關。
湍流
湍流(英語:turbulence),也稱為 紊流(大陸地區的舊稱),是流體的一種流動狀態。當流速很小時,流體分層流動,互不混合,稱為層流,或稱為片流;逐漸增加流速,流體的流線開始出現波浪狀的擺動,擺動的頻率及振幅隨流速的增加而增加,此種流況稱為過渡流;當流速增加到很大時,流線不再清楚可辨,流場中有許多小漩渦,稱為湍流,又稱為亂流(日本及港澳台用字)、擾流或紊流。
這種變化可以用雷諾數來量化。雷諾數較小時,黏滯力對流場的影響大於慣性力,流場中流速的擾動會因黏滯力而衰減,流體流動穩定,為層流;反之,若雷諾數較大時,慣性力對流場的影響大於黏滯力,流體流動較不穩定,流速的微小變化容易發展、增強,形成紊亂、不規則的湍流流場。
流態轉變時的雷諾數值稱為臨界雷諾數。臨界雷諾數與流場的參考尺寸有密切關係。一般管道流雷諾數Re4000為湍流狀態,Re=2100~4000為過渡狀態。
在管路設計中,湍流比層流需要更高的泵輸出功率。而在熱交換器或者反應器設計中,湍流反而有利於熱傳遞或者充分混合。
有效地描述湍流的性質,至今仍然是物理學中的一個重大難題。
流體力學
流體力學(英語:Fluid mechanics)是力學的一門分支,是研究流體(包含氣體、液體及電漿)現象以及相關力學行為的科學。流體力學可以按照研究對象的運動方式分為流體靜力學和流體動力學,前者研究處於靜止狀態的流體,後者研究力對於流體運動的影響。流體力學按照套用範圍,分為:空氣力學及水力學等等。
流體力學是連續介質力學的一門分支,是以巨觀的角度來考慮系統特性,而不是微觀的考慮系統中每一個粒子的特性。流體力學(尤甚是流體動力學)是一個活躍的研究領域,其中有許多尚未解決或部分解決的問題。流體動力學所套用的數學系統非常複雜,最佳的處理方式是利用電腦進行數值分析。有一個現代的學科稱為計算流體力學,就是用數值分析的方式求解流體力學問題。粒子圖像測速技術是一個將流體流場視覺化並進行分析的實驗方式,也利用了流體高度可見化的特點。
參見
•力學
•流固耦合
•空氣動力學
•工程力學
•伯努利定律
