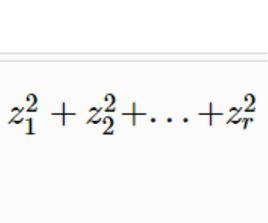基本介紹
復二次型是一類特殊的二次型,複數域C上的二次型,稱為復二次型,任一復二次型φ(x,x,…,x)必與一復規範形的二次型y²+y²+…+y²等價。這裡r是此二次型的秩,兩個復二次型若且唯若它們的秩相同時等價 。
相關介紹及性質
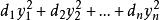 復二次型
復二次型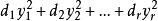 復二次型
復二次型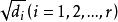 復二次型
復二次型給定一個n元復二次型,可以用一個適當的非退化線性替換,把二次型化成標準形,當原二次型的秩為r(r>0)時,標準形中非零平方項的個數為r,不妨設它的前r個平方項是非零的,那么上述標準形可以寫成,已知二次型的 標準形不唯一,那么能不能在標準形巾找到一個典型代表,使得它具有特別簡單的形式?注意到每一個非零複數有兩個平方根,因此可以選取d的一個平方根,並作右邊的線性替換,顯然這個線性替換是非退化的,它把上述標準形變成
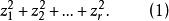 復二次型
復二次型由於二次型的等價關係具有傳遞性,上式也是原二次型的一個標準型,其形式無疑是最簡單的,又由於標準形(1)中非零平方項的個數等於原二次型的秩,而秩是一個不變數,因此標準形(1)是唯—的,稱為 原二次型的復規範形,簡稱為 規範形。當二次型的秩為零時,補充規定,它的規範形為0,這就得到
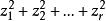 復二次型
復二次型定理1 每一個秩為r(r>0)的n元復二次型都可以經過一個適當的非退化線性替換化成復規範形,並且復規範形是唯一的 。
由於二次型的等價關係具有對稱性和傳遞性,由上述定理立即得到:
推論2 兩個n元復二次型是等價的若且唯若它們有相同的復規範形,或者若且唯若它們有相同的秩。
用矩陣的語言,定理1和推論2可以敘述如下:
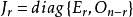 復二次型
復二次型定理3 秩為r(r>0)的n階復對稱矩陣A必契約於J,這裡J是A的相抵標準形,即,稱為A的復規範形,簡稱為規範形。
推論4 兩個n階復對稱矩陣是契約的當且儀當它們有相同的復規範形,或者若且唯若它們有相同的秩。
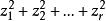 復二次型
復二次型全體n元復二次型按照二次型的等價關係進行分類,一共可以分成n+1類,所有秩為r的n元復二次型恰好構成其中的一個類,因而可以選取復規範形作為這類二次型的代表。
上述結論可以用矩陣的語言敘述如下:全體n階復對稱矩陣按照矩陣的契約關係進行分類,一共可以分成n+1類,所有秩為r的n階復對稱矩陣恰好構成其中的一個類,因而可以選取復規範形J作為這類矩陣的代表 。