徑向基函式簡介
在介紹徑向基網路之前，先簡單介紹一下徑向基函式（Radical Basis Function，RBF）。徑向基函式（Radical Basis Function，RBF）方法是Powell在1985年提出的。所謂徑向基函式，其實就是某種沿徑向對稱的標量函式。通常定義為空間中任一點x到某一中心c之間歐氏距離的單調函式，可記作k(||x-c||)，其作用往往是局部的，即當x遠離c時函式取值很小。例如高斯徑向基函式：
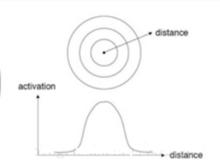圖1 高斯徑向基函式
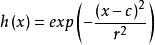徑向基函式網路徑向基函式的誕生主要是為了解決多變數插值的問題。如圖2所示，具體的實現過程是先在每個樣本上面放一個基函式，圖中每個藍色的點是一個樣本，然後中間圖綠色虛線對應的表示的是每個訓練樣本對應一個高斯函式（高斯函式中心就是樣本點）。假設真實的擬合這些訓練數據的曲線是藍色的包絡，如果我們有一個新的數據x1，我們想知道它對應的f(x1)是多少，也就是a點的縱坐標是多少。那么由圖可以看到，a點的縱坐標等於b點的縱坐標加上c點的縱坐標。而b的縱坐標是第一個樣本點的高斯函式的值乘以一個大點權值得到的，c的縱坐標是第二個樣本點的高斯函式的值乘以另一個小點的權值得到。而其他樣本點的權值全是0，因為我們要插值的點x1在第一和第二個樣本點之間，遠離其他的樣本點，那么插值影響最大的就是離得近的點，離的遠的就沒什麼貢獻了。所以x1點的函式值由附近的b和c兩個點就可以確定了。拓展到任意的新的x，這些紅色的高斯函式乘以一個權值後再在對應的x地方加起來，就可以完美的擬合真實的函式曲線了。
圖2 徑向基函式模擬插值過程具體參見：徑向基函式
徑向基網路簡介
到了1988年， Moody和 Darken提出了一種神經網路結構，即RBF神經網路，屬於前向神經網路類型，它能夠以任意精度逼近任意連續函式，特別適合於解決分類問題。
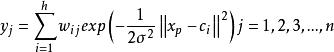徑向基函式網路RBF網路的結構與多層前向網路類似，它是一種三層前向網路。輸入層由信號源結點組成；第二層為隱含層，隱單元數視所描述問題的需要而定，隱單元的變換函式是RBF徑向基函式，它是對中心點徑向對稱且衰減的非負非線性函式；第三層為輸出層，它對輸入模式的作用作出回響。從輸人空間到隱含層空間的變換是非線性的，而從隱含層空間到輸出層空間變換是線性的。
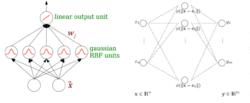徑向基函式網路RBF網路的基本思想是：用RBF作為隱單元的“基”構成隱含層空間，這樣就可將輸入矢量直接（即不需要通過權連線）映射到隱空間。根據Cover定理，低維空間不可分的數據到了高維空間會更有可能變得可分。換句話來說，RBF網路的隱層的功能就是將低維空間的輸入通過非線性函式映射到一個高維空間。然後再在這個高維空間進行曲線的擬合。它等價於在一個隱含的高維空間尋找一個能最佳擬合訓練數據的表面。這點與普通的多層感知機MLP是不同的。
當RBF的中心點確定以後，這種映射關係也就確定了。而隱含層空間到輸出空間的映射是線性的，即網路的輸出是隱單元輸出的線性加權和，此處的權即為網路可調參數。由此可見，從總體上看，網路由輸人到輸出的映射是非線性的，而網路輸出對可調參數而言卻又是線性的。這樣網路的權就可由線性方程組直接解出，從而大大加快學習速度並避免局部極小問題。
從另一個方面也可以這樣理解，多層感知器（包括BP神經網路）的隱節點基函式採用線性函式，激活函式則採用Sigmoid函式或硬極限函式。而RBF網路的隱節點的基函式採用距離函式（如歐氏距離），並使用徑向基函式（如Gaussian函式）作為激活函式。徑向基函式關於n維空間的一個中心點具有徑向對稱性，而且神經元的輸入離該中心點越遠，神經元的激活程度就越低。隱節點的這一特性常被稱為“局部特性”。
RBF網路的設計與求解
RBF的設計主要包括兩個方面，一個是結構設計，也就是說隱藏層含有幾個節點合適。另一個就是參數設計，也就是對網路各參數進行求解。 由上面的輸入到輸出的網路映射函式公式可以看到，網路的參數主要包括三種：徑向基函式的中心、方差和隱含層到輸出層的權值。到目前為止，出現了很多求解這三種參數的方法，主要可以分為以下兩大類：
結構設計
通過非監督方法得到徑向基函式的中心和方差，通過監督方法（最小均方誤差）得到隱含層到輸出層的權值。具體如下：
（1）在訓練樣本集中隨機選擇h個樣本作為h個徑向基函式的中心。更好的方法是通過聚類，例如K-means聚類得到h個聚類中心，將這些聚類中心當成徑向基函式的h箇中心。
（2）RBF神經網路的基函式為高斯函式時，方差可由下式求解：
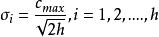徑向基函式網路式中cmax 為所選取中心之間的最大距離，h是隱層節點的個數。擴展常數這么計算是為了避免徑向基函式太尖或太平。
（3）隱含層至輸出層之間神經元的連線權值可以用最小均方誤差LMS直接計算得到，計算公式如下：（計算偽逆）（d是我們期待的輸出值）
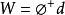徑向基函式網路
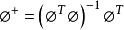徑向基函式網路參數設計
採用監督學習算法對網路所有的參數（徑向基函式的中心、方差和隱含層到輸出層的權值）進行訓練。主要是對代價函式（均方誤差）進行梯度下降，然後修正每個參數。具體如下：
（1）隨機初始化徑向基函式的中心、方差和隱含層到輸出層的權值。當然了，也可以選用結構設計中的（1）來初始化徑向基函式的中心。
（2）通過梯度下降來對網路中的三種參數都進行監督訓練最佳化。代價函式是網路輸出和期望輸出的均方誤差：
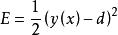徑向基函式網路然後每次疊代，在誤差梯度的負方向已一定的學習率調整參數。
