介紹
神經網路最早由心理學家和神經生物學家提出，由於神經網路在解決複雜問題時能夠提供一種相對簡單的方法，因此近年來越來越受到人們的關注。神經網路模型各種各樣、 各式各樣的模型從不同的角度對生物神經系統進行不同層次的描述和模擬。代表性的網路模型有BP網路、RBF網路、Hopfield網路、自組織特徵映射網路等。運用這些網路模型可實現函式逼近、數據聚類、模式分類、最佳化計算等功能。因此， 神經網路廣泛套用於人工智慧、自動控制、機器人、統計學等領域的信息處理中。
結構
一個經典的神經網路是一個包含三個層次的。紅色的是輸入層，綠色的是輸出層，紫色的是中間層 （也叫隱藏層 ）。輸入層有3個輸入單元，隱藏層有4個單元，輸出層有2個單元。 如圖所示。
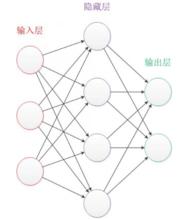神經網路結構設計一個神經網路時，輸入層與輸出層的節點數往往是固定的，中間層則可以自由指定；
神經網路結構圖中的拓撲與箭頭代表著預測過程時數據的流向，跟訓練時的數據流有一定的區別；
結構圖裡的關鍵不是圓圈（代表“神經元”），而是連線線（代表“神經元”之間的連線）。每個連線線對應一個不同的權重（其值稱為權值），這是需要訓練得到的。
除了從左到右的形式表達的結構圖，還有一種常見的表達形式是從下到上來表示一個神經網路。這時候，輸入層在圖的最下方。輸出層則在圖的最上方，如下圖。
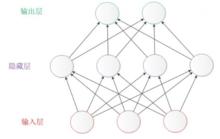神經網路結構種類
BP網路
BP( back propaga tion) 神經網路通常採用基於BP神經元的多層前向神經網路的結構形式。一個典型的BP網路結構如下圖所示。理論證明，具有圖1所示結構的BP神經網路, 當隱層神經元數目足夠多時, 可以以任意精度逼近任何一個具有有限間斷點的非線性函式。
BP神經網路的學習規則, 即權值和閾值的調節規則採用的是誤差反向傳播算法( BP算法)。BP 算法實際上是W idrow -Hoff算法在多層前向神經網路中的推廣。和W idrow- H off算法類似，在BP算法中，網路的權值和閾值通常是沿著網路誤差變化的負梯度方向進行調節的，最終使網路誤差達到極小值或最小值, 即在這一點誤差梯度為零。限於梯度下降算法的固有缺陷，標準的BP學習算法通常具有收斂速度慢、易陷入局部極小值等特點， 因此出現了許多改進算法。其中最常用的有動量法和學習率自適應調整的方法, 從而提高了學習速度並增加了算法的可靠性。
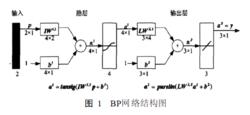神經網路結構RBF神經網路
徑向基函式(Radial Basis Function, 簡稱為RBF) 網路是以函式逼近理論為基礎而構造的一類前向網路，這類網路的學習等價於在多維空間中尋找訓練數據的最佳擬合平面。徑向基函式網路的每個隱層神經元激活函式都構成了擬合平面的一個基函式，網路也由此得名。徑向基函式網路是一種局部逼近網路，即對於輸入空間的某一個局部區域只存在少數的神經元用於決定網路的輸出。而BP網路則是典型的全局逼近網路，即對每一個輸入/輸出數據對，網路的所有參數均要調整。由於二者的構造本質不同，徑向基函式網路與BP網路相比規模通常較大，但學習速度較快，並且網路的函式逼近能力、模式識別與分類能力都優於後者 。
一個典型的徑向基函式網路包括兩層， 即隱層和輸出層。圖2是一徑向基函式網路的結構圖。圖中所示網路的輸入維數為R、隱層神經元個數為S1、輸出個數為S2，隱層神經元用高斯函式作為激活函式， 輸出層的激活函式為線性函式。
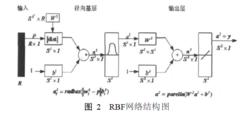神經網路結構由模式識別理論可知，在低維空間非線性可分的問題總可映射到一個高維空間，使其在此高維空間中為線性可分。在RBF網路中，輸入到隱層的映射為非線性的( 隱單元的激活函式是非線性函式)，而隱層到輸出則是線性的。可把輸出單元部分看作一個單層感知器，這樣， 只要合理選擇隱單元數(高維空間的維數)及其激活函式，就可以把原來問題映射為一個線性可分問題，從而最後用一個線性單元來解決問題。最常用的徑向基函式形式是高斯函式， 它的可調參數有兩個，即中心位置及方差( 函式的寬度參數)，用這類函式時整個網路的可調參數(待訓練的參數) 有三組， 即各基函式的中心位置、方差和輸出單元的權值。
RBF網路具有很好的通用性。已經證明，只要有足夠多的隱層神經元，RBF網路能以任意精度近似任何連續函式。更重要的是， RBF網路克服了傳統前饋神經網路的很多缺點，其訓練速度相當快，並且在訓練時不會發生震盪和陷入局部極小。但是，在進行測試時，RBF網路的速度卻比較慢，這是由於待判別示例幾乎要與每個隱層神經元的中心向量進行比較才能得到結果。雖然可以通過對隱層神經元進行聚類來提高判別速度，但這樣就使得訓練時間大為增加，從而失去了RBF網路最基本的優勢。另外，通過引入非線性最佳化技術可以在一定程度上提高學習精度，但這同時也帶來了一些缺陷，如局部極小、訓練時間長等。
Hopfield網路
BP神經網路和RBF網路都是前饋型神經網路，下面我們研究反饋式神經網路。在反饋式網路中，所有節點(單元)都是一樣的， 它們之間可以相互連線， 所以反饋式神經元網路可以用一個無向的完備圖來表示。從系統觀點來看，反饋網路是一個非線性動力學系統。它必然具有一般非線性動力學系統的許多性質，如穩定問題、各種類型的吸引子以至混沌現象等。在某些情況下， 還有隨機性和不可預測性等，因此，比前饋型網路的內容要廣闊和豐富的多，提供了人們可以從不同方面來利用這些複雜的性質以完成各種計算功能。
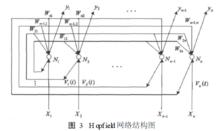
反饋式網路的模型有多種， 這裡主要討論由Hopfield提出的反饋網路。Hopfield網路的基本結構圖如圖3所示。
神經網路結構由圖3可見Hopfield 網路為一層結構的反饋網路，能處理雙極型離散數據。當網路經過訓練後， 可以認為網路處於等待工作狀態，而對網路給定初始輸入x 時， 網路就處於特定的初始狀態， 由此初始狀態開始運行，可以得到當前時刻網路的輸出狀態。通過網路的反饋作用，可得到下一時刻網路的輸入信號；再由這個新的輸入信號作用於網路，可得到下一時刻網路的輸出狀態，將該輸出反饋到輸入端，又形成新的輸入信號，如此不斷的循環下去。如果網路是穩定的，那么， 經過多次反饋運行， 網路達到穩態， 即由輸出端可得到網路的穩態輸出。
反饋網路有兩種基本的工作方式：串列異步和並行同步方式。反饋式和前饋型神經網路的比較如下：
(1) 前饋型神經網路取連續或離散變數，一般不考慮輸出與輸入在時間上的滯後效應， 只表達輸出與輸入的映射關係。反饋式神經網路可以用離散變數也可連續取值， 考慮輸出與輸入之間在時間上的延遲， 因此， 需要用動態方程來描述神經元和系統的數學模型。由於前饋網路中不含反饋連線， 因而為系統分析提供了方便。基本的H opfield網路是一個由非線性元件構成的單層反饋系統， 這種系統穩定狀態的分析比較複雜， 給實際套用帶來一些困難。
(2) 前饋型網路的學習主要採用誤差修正法， 計算過程一般比較慢， 收斂速度也比較慢。而Hopfield 網路的學習主要採用Hebb規則， 一般情況下計算的收斂速度很快。它與電子電路存在明顯的對應關係， 使得該網路易於理解和易於用硬體實現。
(3)Hopfield網路也有類似於前饋型網路的套用， 例如用作聯想記憶或分類， 而在最佳化計算方面的套用更加顯示出Hopfield 網路的特點。聯想記憶和最佳化計算是對偶的。當用於聯想記憶時，通過樣本模式的輸入給定網路的穩定狀態， 經過學習求得突觸權重值; 當用於最佳化計算時， 以目標函式和約束條件建立系統的能量函式確定出突觸權重值， 網路演變到穩定狀態， 即是最佳化計算問題的解。
自組織特徵映射網路
自組織特徵映射模型也稱為Kohonen網路， 或者稱為Self-Organizing Feature Map ( SOFM) ， 由芬蘭學者Teuvo Kohonen 於1981年提出。該網路是一個由全互連的神經元陣列形成的無教師自組織自學習網路。
Kohonen認為， 處於空間中不同區域的神經元有不同的分工， 當一個神經網路接受外界輸入模式時， 將會分為不同的反應區域， 各區域對輸入模式具有不同的回響特徵。在輸出空間中， 這些神經元將形成一張映射圖， 映射圖中功能相同的神經元靠得較近， 功能不同的神經元分得較開， 自組織特徵映射網路也由此而得名。它在模式識別、聯想存儲、樣本分類、最佳化計算、機器人控制等領域中得到廣泛套用。自組織特徵映射過程是通過競爭學習完成的。競爭學習是指同一層神經元之間互相競爭， 競爭勝利的神經元修改與其相連的連線權值的過程。競爭學習是一種無監督學習方法， 在學習過程中， 只需向網路提供一些學習樣本， 而無需提供理想的目標輸出。網路根據輸入樣本的特性進行自組織映射， 從而對樣本進行自動排序和分類。
套用
神經網路是一門重要的機器學習技術。它是目前最為火熱的研究方向深度學習的基礎。神經網路在系統辨識、模式識別、智慧型控制等領域有著廣泛而吸引人的前景。特別在智慧型控制中，人們對神經網路的自學習功能尤其感興趣，並且把神經網路這一重要特點看作是解決自動控制中按制器適應能力這個難題的關鍵鑰匙之一。 神經網路的基礎在於神經元。神經元是以生物神經系統的神經細胞為基礎的生物模型。在人們對生物神經系統進行研究，以探討人工智慧的機制時，把神經元數學化，從而產生了神經元數學模型。 大量的形式相同的神經元連結在—起就組成了神經網路。神經網路是一個高度非線性動力學系統。雖然，每個神經元的結構和功能都不複雜，但是神經網路的動態行為則是十分複雜的；因此，用神經網路可以表達實際物理世界的各種現象。神經網路模型是以神經元的數學模型為基礎來擁述的。神經網路模型由網路拓撲、節點特點和學習規則來表示。
