強穩定性

強穩定性是一種較強的穩定性質。如果能證明有有界解是強穩定的，那么它就是概周期解；反之，在微分方程滿足標準假設時，方程的任何概周期解都是強穩定的。

簡介

強穩定性是一種較強的穩定性質。

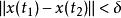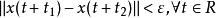強穩定性

強穩定性

如果對任給 ε>0 ，存在 δ(ε)>0 ，使得只要，便有，稱解 x(t) 是強穩定的。

如果能證明有有界解是強穩定的，那么它就是概周期解；反之，在微分方程滿足標準假設時，方程的任何概周期解都是強穩定的。

可繼承性

(inherited property)

可繼承性是關於一致概周期微分方程解的一種重要性質。

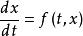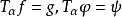強穩定性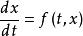

強穩定性

強穩定性

如果一致概周期微分方程的解 φ(x) 相對於其他解具有性質 P ，若， 而ψ(t) 相對於的解也具有性質 P ，則稱性質 P 是可繼承的。也就是說，若解φ(x)具有可繼承的性質 P ，那么，性質 P 在運算元 T的作用下是自封的。

通常往往利用有界解的某些穩定性質來建立有界解的概周期性，諸如一致穩定、一致漸近穩定、完全穩定或殼擾動下的穩定等，這些穩定性質在方程滿足標準假設時都是可繼承的。