基本介紹
幾何透視法是把幾何透視運用到繪畫之中,是科學與藝術相結合的表現技法。它主要藉助於近大遠小的透視現象表現物象的立體感 。
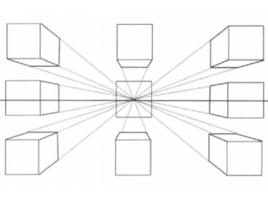
 圖1 透視規律
圖1 透視規律幾何透視法三要素
幾何透視法包括三個要素 :
視平線
視平線一般是指畫者平視時與眼睛高度平行的假設線。視平線決定被畫物的透視斜度,被畫物高於視平線時,透視線向下傾斜,被畫物低於視平線時,透視線向上傾斜。
中心點
中心點是指視覺的中心。它位於被畫物的核心部位。在平行透視中,一切透視線都將引向中心點。中心點也被稱為消失點、滅點。
距點
視點至中心點的距離叫 視距,如果把視距移至視平線上中心點的兩側。所得的點為 距點。
幾何透視法三大類
幾何透視法有三大分類: 一點透視、 兩點透視以及 三點透視。
一點透視
一點透視又稱為 平行透視,由於在透視的結構中,只有一個透視消失點,而沒有延伸的線條相互平行,從而被稱為一點透視。
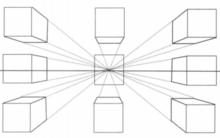 圖2
圖2一點透視法可將物象的多個面表現出立體感,但是只有立體感是不夠的,在真正的場景中,最重要的是要表現出物象各面一致的遠近感。
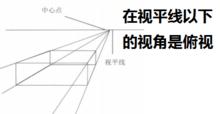 圖3
圖3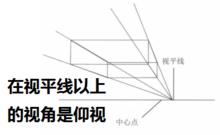 圖4
圖4 圖5
圖5兩點透視
如果一個畫面中有兩個中心點,而且這兩個點都在視平線上,那么這樣形成的透視被稱為 兩點透視。
兩點透視,即成角透視。在一點透視中假設所有的物象都是平行擺放的,而實際物象與畫面常常會形成一定的角度,因此運用兩點透視就能更準確地表現出每一個物象。
兩點透視的效果比較自由、活潑,給人造成的空間感也接近於人對真實空間的感覺,但透視角度不好選擇,容易產生變形 。
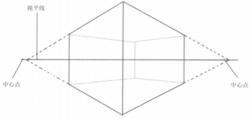 圖6
圖6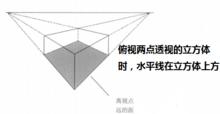 圖7
圖7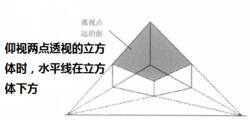 圖8
圖8 圖9
圖9三點透視
如果畫面中有三個中心點,其中有兩個點在水平線上,那么這樣形成的透視圖被稱為三點透視 。
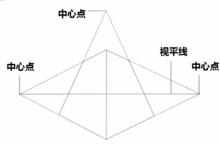 圖10
圖10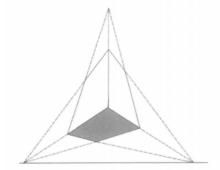 圖11
圖11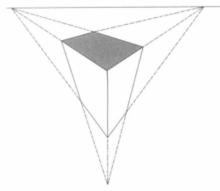 圖12
圖12三點透視一般用於繪製大面積場景的俯瞰圖或仰視圖,它是一點透視和兩點透視的集合體 。
 圖13
圖13