簡介
幾何三大問題(Three major geometric problems),亦稱尺規作圖問題,源於古希臘是幾何學中的著名問題,主要包括尺規作圖三大問題 :
(1)三等分角問題:即把任意一個已知角三等分;
(2)立方倍積問題:即求作一個立方體,使它的體積等於已知立方體的體積的2倍;
(3)化圓為方問題:也稱圓積問題,即求作一個正方形,使它的面積等於一個已知圓的面積。
這三個問題吸引了歷代許多學者進行研究,長期未能解決,被稱為 幾何三大問題。直至1837年,Wantzel用代數方法首先證明了(1)、(2)兩個問題均屬尺規作圖不能問題。1882年,林德曼(Lindemann)證明了第三個問題也屬於尺規作圖不能問題.1895年,克萊因(Klein, (C. )F.)總結了前人的研究,著有《幾何三大問題》一書,給出三大問題不可能用尺規來作圖的簡明證法,徹底解決了兩千多年的懸案。如果不限制作圖工具,幾何三大問題根本就不是什麼難題,而且早已解決。公元前5世紀,雅典的智人學派以上述三大問題為中心開展研究,正因為問題不能用尺規來解決,常常使人進人新的領域中去,促進了數學的發展.如激發了圓錐曲線、割圓曲線以及三、四次代數曲線的出現。
內容
三等分角問題
三等分角問題的完整敘述為:在只用圓規及一把沒有刻度的直尺將一個給定角三等分。在尺規作圖(指用沒有刻度的直尺和圓規作圖)的前提下,此題無解。若將條件放寬,例如允許使用有刻度的直尺,或者可以配合其他曲線使用,可以將一給定角分為三等分 。
立方倍積問題
 幾何三大問題
幾何三大問題 幾何三大問題
幾何三大問題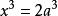 幾何三大問題
幾何三大問題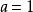 幾何三大問題
幾何三大問題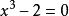 幾何三大問題
幾何三大問題立方倍積問題(problem of duplication of a cube)亦稱倍立方體問題、德里安問題、Delos問題、德洛斯問題 、第羅斯問題等,是幾何三大問題之一。假設已知立方體的棱長為,所求立方體的棱長為,則,令,有。可以證明,若此方程有有理根,不外乎±1,±2,但它們都不是方程的根,因而不存在有理根,根據“有理係數的三次方程若無有理根,則長度等於它的任何實根的線段不能僅用尺規作圖”的定理,立方倍積屬尺規作圖不能問題。
化圓為方問題
 幾何三大問題
幾何三大問題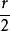 幾何三大問題
幾何三大問題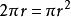 幾何三大問題
幾何三大問題化圓為方問題(problem of quadrature of circle),也稱圓積問題,由古希臘著名學者阿納克薩戈勒斯提出的,但是阿納克薩戈勒斯一生也未能解決自己提出的問題。該問題為求作一個正方形,使其面積等於已知圓的面積,其難度在於作圖使用工具的限制。若不受標尺的限制,化圓為方問題並非難事,歐洲文藝復興時代的大師,義大利數學家達文西(1452-1519)用已知圓為底,圓半徑的為高的圓柱,在平面上滾動一周,所得的矩形,其面積恰為圓的面積,所得矩形的面積為,,然後再將矩形化為等積的正方形即可 。
意義
雖然三大幾何作圖難題都被證明是不可能由尺規作圖的方式做到的,但是為了解決這些問題,數學家們進行了前赴後繼的探索,最後得到了不少新的成果,發現了許多新的方法。同時,它反映了數學作為一門科學,它是一片浩瀚深邃的海洋,仍有許多未知的謎底等待這我們去發現。
