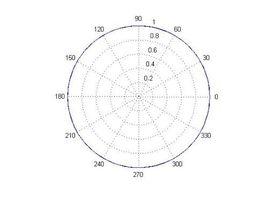
定義
正如所有的二維坐標系,平面極坐標系也有兩個坐標軸:r(半徑坐標)和θ(角坐標、極角或方位角,有時也表示為φ或t)。r坐標表示與極點的距離,θ坐標表示按逆時針方向坐標距離0°射線(有時也稱作極軸)的角度,極軸就是在平面直角坐標系中的x軸正方向。比如,極坐標中的(3,60°)表示了一個距離極點3個單位長度、和極軸夾角為60°的點。(−3,240°) 和(3,60°)表示了同一點,因為該點的半徑為在夾角射線反向延長線上距離極點3個單位長度的地方(240°−180°=60°)。極坐標系中一個重要的特性是,平面直角坐標中的任意一點,可以在極坐標系中有無限種表達形式。通常來說,點(r,θ)可以任意表示為(r,θ±n×360°)或(−r,θ ±(2n+1)180°),這裡n是任意整數。如果某一點的r坐標為0,那么無論θ取何值,該點的位置都落在了極點上。
使用弧度單位
極坐標系中的角度通常表示為角度或者弧度,使用公式2π rad = 360°。具體使用哪一種方式,基本都是由使用場合而定。航海(Navigation)方面經常使用角度來進行測量,而物理學的某些領域大量使用到了半徑和圓周的比來作運算,所以物理方面更傾向使用弧度。
極坐標系
在極坐標中,x被 ρcosθ代替,y被 ρsinθ代替。 ρ=(x+y)。極坐標系是一個二維坐標系統。該坐標系統中的點由一個夾角和一段相對中心點—極點(相當於我們較為熟知的直角坐標系中的原點)的距離來表示。極坐標系的套用領域十分廣泛,包括數學、物理、工程、航海以及機器人領域。在兩點間的關係用夾角和距離很容易表示時,極坐標系便顯得尤為有用;而在平面直角坐標系中,這樣的關係就只能使用三角函式來表示。對於很多類型的曲線,極坐標方程是最簡單的表達形式,甚至對於某些曲線來說,只有極坐標方程能夠表示。
在極坐標系與平面直角坐標系間轉換
極坐標系中的兩個坐標r和θ可以由下面的公式轉換為直角坐標系下的坐標值:x=r*cos(θ),y=r*sin(θ)。由上述二公式,可得到從直角坐標系中x和y兩坐標如何計算出極坐標下的坐標:r=sqrt(x +y ),θ=arctany/x。在x=0的情況下:若y為正數θ=90°(π/2 radians);若y為負,則θ=270°(3π/2 radians)。
極坐標方程
用極坐標系描述的曲線方程稱作極坐標方程,通常用來表示r為自變數θ的函式。極坐標方程經常會表現出不同的對稱形式,如果r(−θ)=r(θ),則曲線關於極點(0°/180°)對稱,如果r(π-θ) = r(θ),則曲線關於極點(90°/270°)對稱,如果r(θ−α)=r(θ),則曲線相當於從極點逆時針方向旋轉α°。
發展史
第一個用極坐標來確定平面上點的位置的是牛頓。他的《流數法與無窮級數》,大約於1671年寫成,出版於1736年。此書包括解析幾何的許多套用,例如按方程描出曲線,書中創見之一,是引進新的坐標系。17甚至18世紀的人,一般只用一根坐標軸(x軸),其y值是沿著與x軸成直角或斜角的方向畫出的。牛頓所引進的坐標之一,是用一個固定點和通過此點的一條直線作標準,例如極坐標系。牛頓還引進了雙極坐標,其中每點的位置決定於它到兩個固定點的距離。由於牛頓的這個工作直到1736年才為人們所發現,而瑞士數學家J.貝努力利於1691年在《教師學報》上發表了一篇基本上是關於極坐標的文章,所以通常認為J.貝努利是極坐標的發現者。J.貝努利的學生J.赫爾曼在1729年不僅正式宣布了極坐標的普遍可用,而且自由地套用極坐標去研究曲線。他還給出了直角價值到極坐標的變換公式。確切地講,J.赫爾曼把cos、sin當作變數來使用,而且用z,n和m來表示cos和sin。歐拉擴充了極坐標的使用範圍,而且明確使用三角函式的記號;歐拉那個時候的極坐標系實際上就是現代的極坐標系。
套用
有些幾何軌跡問題如果用極坐標法處理,它的方程比用直角坐標法來得簡單,描圖也較方便。1694年,J.貝努利利用極坐標引進了雙紐線,這曲線在18世紀起了相當大的作用。
典型圖像模型例舉與解析;圓心原點的時候;圓與坐標軸相切的時候。
平面極坐標系下動量算符的選擇
動量算符是量子力學中的基本算符。量子力學中的所有力學量用力學量用厄米算符表示。若在經典力學中有相應的力學量,則在量子力學中表示這個力學量的算符由經典表示式中將動量換為算符-ih得出。更一般地,對於笛卡爾坐標中的一維情況,當存在經典類比時,動量算符應為
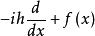 平面極坐標
平面極坐標但對於非笛卡爾坐標,如平面極坐標和球面坐標系,動量算符的整體形式及各方向分量形式卻很容易讓人產生誤解,這在一般的量子力學教材中幾乎沒有提及。尹世忠給出了球坐標系下的動量算符各分量的具體表達式,但對於算符的構造方法介紹較為簡略,也沒有給出平面極坐標系下的動量算符。本文利用“對稱法”及力學量算符的厄米性構造出平面極坐標系動量算符各方向的分量。
拉普拉算符在平面極坐標系下的表達式
極坐標與二維直角坐標系轉換關係如下:
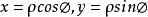 平面極坐標
平面極坐標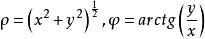 平面極坐標
平面極坐標逆變換關係為:
動量算符各分量式在平面極坐標系下的選擇
(1)從動能算符判定
一個具有旋轉對稱的二維運動粒子,在二維指教坐標系中的動能算符為:
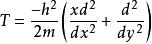 平面極坐標
平面極坐標(2)從厄米性判定
量子力學的所有力學量算符必須是線性厄米算符。此二算符線性顯然滿足,因此,需要考查這兩個算符的厄米性。由直角坐標系與極平面極坐標系的相互轉換關係有:
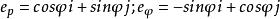 平面極坐標
平面極坐標研究結論
(1)直角坐標系下動量算符各分量的表述形式並不適用於極坐標系。
(2)對於直角坐標系中的動量算符分量,即其後可加上有關該方向坐標的函式不影響原來的算符,但在非笛卡兒坐標系中卻不成立。
(3)動量算符應和正則共軛動量對應,而不是和機械動量m→v對應。
(4)在對力學量進行量子化過程中,當存在經典類比時,從任一經典力學量F(→r,→p)去構造相應的量子力學算符時,即使在坐標表象中,也不能只單純地做→r→r,→p→-ih替換,必須保證所構造出的算符的厄米性,恰當的方法就是利用“對稱化”。